Em alguns sistemas, um cliente é alocado a uma de duas instalações. Se o tempo de serviço de um cliente servido por uma instalação i tiver uma distribuição com parâmetros i (i 1, 2) e p for a proporção de todos os clientes servidos pela instalação 1, a fdp de X tempo de serviço de um cliente selecionado aleatoriamente será
Passo 1
- O pdf é dado a nós como:
- Recordamos a definição de cdf de uma variável contínua.
- Vamos denotar a mediana como e sabemos que na mediana:
- É dado que Y é o número entre os dez laboratórios em que a temperatura excede 1. Então
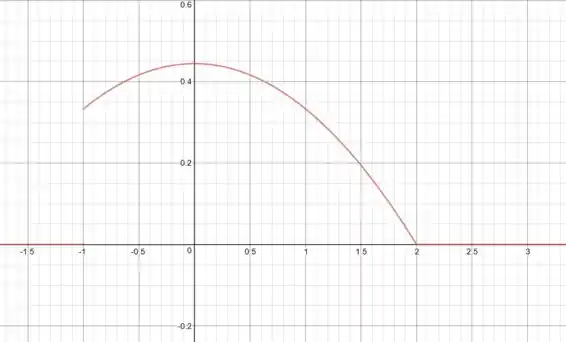
Ela está representada na figura abaixo:
Definição: A função de distribuição cumulativa F(x) para uma rv contínua X é definida para cada número x por
Como é diferente de zero apenas para x entre -1 e 2. Portanto, para qualquer x entre -1 e 2, podemos escrever:
Desta forma global F(X) pode ser dado como:
O cdf é plotado na figura abaixo:

Passo 2
Do cdf que derivamos na última parte:
Portanto, 0 não é a temperatura mediana na qual a reação ocorre.
E uma vez que:
Portanto, a temperatura mediana é maior que 0.
Passo 3
E p é a probabilidade de que a temperatura em um laboratório exceda 1. Portanto
Proposição: Seja X uma va contínua com pdf f(x) e cdf F(x). Então, para qualquer número a,
Resposta
b)
c) Não, a temperatura mediana é maior do que 0
d)