Me chamo Yuri e hoje estarei aqui para lhe ajudar a resolver mais uma atividade com o padrão de qualidade do responde aí. Vem comigo!!!!

É dado que Y é a distância da extremidade esquerda na qual ocorre a quebra. Também é dado que Y tem pdf f(y), escrito como:

1. Recordamos a definição de cdf de uma variável contínua.

Definição: A função de distribuição cumulativa F(y) para uma rv contínua Y é definida para cada número y por

Para qualquer número y entre 0 e 12

Assim, F(y) pode ser dado como:

O cdf F(Y) é plotado na figura abaixo:



2. Calculando

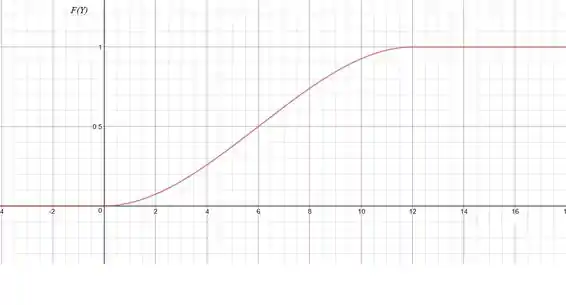
Calculado

Passo 2

Calculando

Proposição: Seja X uma va contínua com pdf f(x) e cdf F(x). Então, para qualquer número a

3. O valor médio da distribuição dada pode ser dado como:

Como já calculamos E(X) na última parte: E(Y) = 6, portanto, usamos a seguinte proposição:

Podemos escrever:

Passo 3

4. Como o ponto de interrupção esperado é calculado como 6 polegadas na última parte, portanto, a probabilidade de que o ponto de interrupção ocorra a mais de 2 polegadas do ponto de interrupção esperado podem ser representadas como .

Este evento é o complemento do evento em que o ponto de interrupção ocorre dentro de 2 polegadas do ponto de interrupção esperado. Por isso

5. Seja X a variável aleatória que denota o comprimento do segmento mais curto quando ocorre a quebra. Então podemos escrever X em termos de Y como:

Portanto, o valor esperado de X pode ser escrito como:

Pulando todas as contas dessas integrais, que não são o nosso foco, temos que