Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 66

Uma amiga que vive em Los Angeles faz viagens frequentes de consultoria para Washington, D.C. Cinquenta por cento das vezes ela viaja pela linha aérea no 1, 30 % das vezes pela no 2 e os 20 % restantes das vezes pela no 3. Na linha no 1, os vôos para Washington atrasam 30% das vezes e para L.A., 10% das vezes. Na linha aérea no 2, essas porcentagens são 25% e 20%, enquanto na linha aérea no 3 são 40% e 25%. Se soubermos que em uma viagem ela chega atrasada em exatamente um dos destinos, quais são as probabilidades posteriores de ela ter voado nas linhas no 1, no 2 e no 3? (Sugestão: Na extremidade de cada ramo de primeira geração em um diagrama de árvore, desenhe três ramos de segunda geração denominados 0 atrasado, l atrasado e 2 atrasado.)

Passo 1

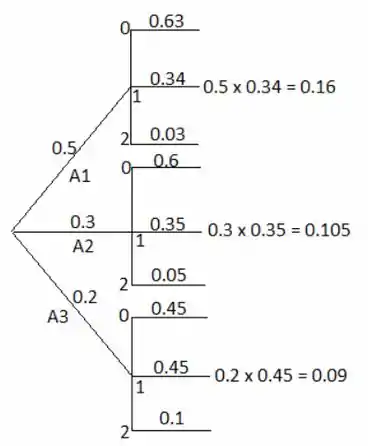
Falaaa, meu querido/minha querida. Como vai?? O diagrama de árvore que representa a situação experimental dada no exercício é dado abaixo.As ramificações iniciais representam a primeira camada de eventos e as probabilidades adequadas são dadas no diagrama. As ramificações de segunda geração representam a segunda camada de eventos, com as probabilidades condicionais adequadas dadas.Usando a regra de multiplicação dada acima, à direita dos ramos de segunda geração, exibimos o produto de probabilidades particulares que levam a esse ponto, que na verdade são as probabilidades das interseções. Então, bora lá para os cálculos!!!

Passo 2

A primeira camada do evento são:

A 1 = { l i n h a   a é r e a   1 }

A 2 = { l i n h a   a é r e a   2 }

A 3 = { l i n h a   a é r e a   3 }

E os eventos da segunda camada são sugeridos no exercício como, respectivamente, 0 atrasado, 1 atrasado e 2 atrasado.

D C = { v o o   a t r a s a d o   p a r a   D C }

L A = { v o o   a t r a s a d o   p a r a   L A }

E as probabilidades adequadas para a primeira camada são:

P A 1 = 0,5

P A 2 = 0,3

P A 3 = 0,2

Agora, as probabilidades condicionais para A 1 são:

P 0 A 1 = P [ D C ∪ L A ' ]

= P [ D C ' ] ∙ P [ L A ' ]

= 0,7 ∙ 0,9

P 0 A 1 = 0,63

P 1 A 1 = P D C ' ∩ L A ∪ D C ∩ L A '

= P D C ' ∙ P L A + P ( D C ) ∙ P L A '

= 0,7 ∙ 0,1 + 0,3 ∙ 0,9

P 1 A 1 = 0,34

2 A 1 = P ( D C ∩ L A )

= P ( D C ) ∙ P ( L A )

= 0,3 ∙ 0,1

P 2 A 1 = 0,03

As probabilidades condicionais para A 2 :

P 0 A 2 = P [ D C ∪ L A ' ]

= P [ D C ' ] ∙ P [ L A ' ]

= 0,75 ∙ 0,8

P 0 A 2 = 0,6

P 1 A 2 = P D C ' ∩ L A ∪ D C ∩ L A '

= P D C ' ∙ P L A + P ( D C ) ∙ P L A '

= 0,75 ∙ 0,2 + 0,25 ∙ 0,8

P 1 A 2 = 0,35

2 A 2 = P ( D C ∩ L A )

= P ( D C ) ∙ P ( L A )

= 0,25 ∙ 0,2

P 2 A 2 = 0,03

Por fim, as probabilidades condicionais para A 3 .

P 0 A 3 = P [ D C ∪ L A ' ]

= P [ D C ' ] ∙ P [ L A ' ]

= 0,6 ∙ 0,75

P 0 A 3 = 0,45

P 1 A 3 = P D C ' ∩ L A ∪ D C ∩ L A '

= P D C ' ∙ P L A + P ( D C ) ∙ P L A '

= 0,6 ∙ 0,25 + 0,4 ∙ 0,75

P 1 A 3 = 0,45

2 A 3 = P ( D C ∩ L A )

= P ( D C ) ∙ P ( L A )

= 0,4 ∙ 0,25

P 2 A 3 = 0,1

O diagrama de árvore também contém as probabilidades das interseções. Usamos a regra da multiplicação para calcular as interseções que precisamos exibir na árvore:

P A 1 ∩ 1 = P A 1 ∙ P 1 A 1 = 0,5 ∙ 0,34 = 0,17

P A 2 ∩ 1 = P A 2 ∙ P 1 A 2 = 0,3 ∙ 0,35 = 0,105

P A 3 ∩ 1 = P A 3 ∙ P 1 A 3 = 0,2 ∙ 0,45 = 0,09

Portanto, a nossa árvore de probabilidades é definida por:

Passo 3

Agora, estamos quase finalizando a questão, precisamos antes calcular a probabilidade de exatamente 1 avião estar atrasado.

P 1 = P A 1 ∙ P 1 A 1 + P A 2 ∙ P 1 A 2 + P ( A 3 ) ∙ P ( 1 | A 3 )

= P A 1 ∩ 1 + P A 2 ∩ 1 + P ( A 3 ∩ 1 )

= 0,17 + 0,105 + 0,09

P 1 = 0,365

Finalmente, as probabilidades posteriores são dadas por:

P A 1 1 = P A 1 ∩ 1 P ( 1 ) = 0,17 0,365 = 0,466

P A 2 1 = P A 2 ∩ 1 P ( 1 ) = 0,105 0,365 = 0,288

P A 3 1 = P A 3 ∩ 1 P ( 1 ) = 0,09 0,365 = 0,247

Resposta

P A 1 1 = 0,466

P A 2 1 = 0,288

P A 3 1 = 0,247

Exercícios de Livros Relacionados

Em dias chuvosos, Joe chega atrasado ao trabalho com probabilidade 0,3; em dias não chuvosos, ele chega atrasado com probabilidade 0,1. Com probabilidade 0,7 choverá amanhã.(a) Determine a probabilida
A probabilidade de fechamento do i-ésimo relé nos circuitos mostrados na Figura 3.4 é p i , i = 1,2,3,4,5. Se todos os relés funcionam independentemente, qual é a probabilidade de que uma corrente flu
As lojas A, B e C tem 50, 75 e 100 empregados, respectivamente, e 50,60 e 70% deles são mulheres, respectivamente. Pedidos de demissão ocorrem de forma igualmente provável entre todos os empregados, i
Suponha que um baralho comum de 52 cartas seja embaralhado e que suas cartas sejam então viradas uma a uma até que o primeiro ás apareça. Dado que o primeiro ás é a vigésima carta a aparecer, qual é a
Há uma chance de 50-50 de que a rainha seja portadora do gene da hemofilia. Se ela é portadora, então cada um dos príncipes tem uma chance de 50-50 de ter hemofilia. Se a rainha tiver tido três prínci