Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 67
No Exercício 59, considere as informações adicionais a seguir sobre a utilização de cartões de crédito:
70% de todos os clientes da gasolina comum que enchem o tanque usam um cartão de crédito.
50% de todos os clientes da gasolina comum que não enchem o tanque usam um cartão de crédito.
60% de todos os clientes da gasolina extra que enchem o tanque usam um cartão de crédito.
50% de todos os clientes da gasolina extra que não enchem o tanque usam um cartão de crédito.
50% de todos os clientes da gasolina premium que enchem o tanque usam um cartão de crédito.
40% de todos os clientes da gasolina premium que não enchem o tanque usam um cartão de crédito.
Calcule a probabilidade de cada um dos eventos a seguir para o próximo cliente a ser atendido (um diagrama de árvore pode ajudar).
a. {extra, tanque cheio e cartão de crédito}
b. {premium, não tanque cheio e cartão de crédito}
c. {premium e cartão de crédito}
d. {tanque cheio e cartão de crédito}
e. {cartão de crédito}
f. se o próximo cliente usar cartão de crédito, qual a probabilidade de que seja pedida a gasolina premium?
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Por exercícios anteriores podemos montar o seguinte diagrama para o nosso exemplo:
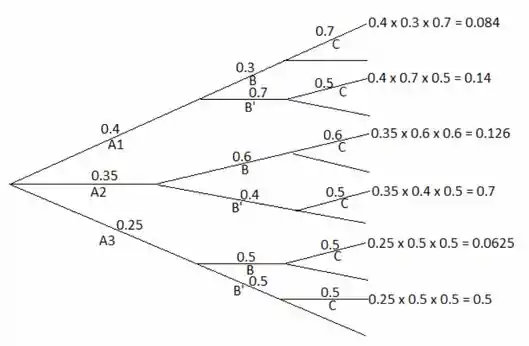
Então, agora temos o que precisamos para calcular as probabilidades. Bora láaa!!!
Passo 2
O evento extra, tanque cheio e cartão de crédito são uma intersecção desses eventos.
Passo 3
O evento premium, não tanque cheio e cartão de crédito também é uma intersecção.
Passo 4
A intersecção dos eventos premium e cartão de crédito é:
Passo 5
A intersecção dos eventos tanque cheio e cartão de crédito é:
Passo 6
A probabilidade de apenas cartão de crédito pode ser calculada usando a Lei da Probabilidade Total. Sendo assim, a probabilidade fica:
Passo 7
Por fim, se o próximo cliente usar um cartão de crédito, a probabilidade de que o prêmio tenha sido solicitado é a probabilidade condicional de dado que o evento ocorreu
Resposta
Resolução nos passos anteriores.