Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 51

Uma amostra aleatória de 5726 números de telefone de uma região, adquiridos em março de 2002, mostrou que 1105 não estavam incluídos na lista e 1 ano depois, uma amostra de 5384 mostrou 980 números não-listados. a. Faça o teste no nível 0,10 para ver se há uma diferença nas proporções reais de números não-listados entre os dois anos. b. Se p1 0,20 e p2 0,18, que tamanhos das amostras (m n) seriam necessários para detectar tal diferença com probabilidade de 0,90?

Passo 1

  1. Dado que p 1 ≠ p 2

    2. A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula afirma uma igualdade. Como a hipótese nula não é a afirmação, a hipótese alternativa é a afirmação

    H 0   : p 1 = p 2

    H a   : p 1   ≠ p 2

    A proporção da amostra é o número de sucessos dividido pelo tamanho da amostra:

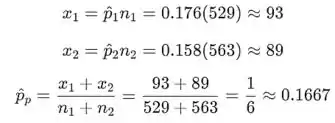
    Os valores críticos são os valores correspondentes a uma probabilidade de 0 . 025 / 0 . 975 na tabela A.3:

    z =   ± 1.96

    A região de rejeição contém todos os valores abaixo de - 1 . 96 e todos os valores acima de 1.96.

    Determine o valor da estatística de teste:

    Se o valor da estatística de teste estiver dentro da região de rejeição, então a hipótese nula é rejeitada:

    - 1.96 < 0.80 < 1.96   → F a l h o u   e m   r e i j e i t a r   H 0

    Não há evidências suficientes para apoiar a afirmação de que a taxa de incidência de problemas gastrointestinais para aqueles que consomem chips olestra de acordo com o regime experimental difere da taxa de incidência para o grupo controle TG

    Passo 2

  2. p 1 = 15 % = 0.15

p 2 = 20 % = 0.20

P   r e j e i t a r   H 0   H 0   f a l s o ) = 0.90

q 1 é o complemento de p 1 e q 2 é o complemento de p 2 .

q 1 = 1 - p 1 = 1 - 0.15 = 0.85

q 2 = 1 - p 2 = 1   0.20 = 0.80

β é a probabilidade de não rejeitar a hipótese nula quando a hipótese nula H 0 é falso (use a regra do complemento):

β = 1 - P R e j e i t a r   H 0   H 0   f a l s o )   1 - 0.90 = 0.10

O valor crítico do nível de significância \alphaα é o valor correspondente a uma probabilidade de α / 2 = 0 . 025 na tabela A.3:

z α 2 = 1.96

O valor crítico da probabilidade de um erro tipo II β é o valor correspondente a uma probabilidade de 0,10 na tabela A.3:

z β = 1.28

d é a diferença nas médias populacionais:

d = p 1 - p 2 = 0.15 - 0.20 = - 0.05

Tamanho da amostra da fórmula:

n = z α 2 p 1 + p 2 q 1 + q 2 2 + z β p 1 q 1 + p 2 q 2 2 d ²

Preencha os valores conhecidos e avalie (arredondando para cima!):

n = 1.96 0.15 + 0.20 0.85 + 0.80 2 + 1.28 0.15 0.85 + 0.20 0.80 2 - 0.05 2 ≈ 1211

Resposta

  1. Não há evidências suficientes para apoiar a afirmação de que a taxa de incidência de problemas gastrointestinais para aqueles que consomem chips olestra de acordo com o regime experimental difere da taxa de incidência para o grupo controle TG.
  2. n = 1211

Exercícios de Livros Relacionados

Um artigo na revista Journal of sports science apresenta resultados de uma investigação do nível de hemoglobina dos jogadores de hóquei no gelo nas olimpíadas do Canadá. Os dados recortados em (g/dl)
Considere o intervalo de confiança para μ , com desvio padrão conhecido σ : x _ - z α 1 s / n μx _ + z α 2 s / n sendo α 1 + α 2 = α . Seja α = 0.05 e encontre o intervalo para α 1 = α 2 = α / 2 = 0.0
Considere e teste de impacte Izod descrito no Exercicio 8.24. Calcule um intervalo de tolerância de 99% para a resisténcia ao impacto de tubos de PVC que tem um nivel de confianca de 90%. Compare o co
Considere os dados de diâmetro de Exercicie 8.34. Calcule um intervalo de telerancia de 95% para o diâmetro des bastecs descrites que tem um nivel de confiança de 90%. Compare 0 comprimento de interva
Em relação ao Exercício 9.43, determine um intervalo de confiança de 99% para se um pneu de cada marca for atribuído aleatoriamente para cada uma das rodas traseiras de oito táxis e as distâncias, em