Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 45
Consulte o Exercício 41 e calcule a estimativa de intervalo para a diferença entre o tempo médio real da tarefa sob o nível de iluminação alto e o tempo médio real sob o nível baixo.
Passo 1
- Dado:
- Gráfico de probabilidade normal
Vou calcular um intervalo de confiança de 95%. Outros limites de confiança podem ser obtidos de forma semelhante.
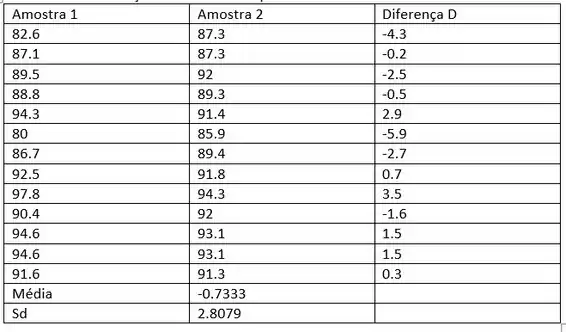
Determine a diferença de valor de cada par.
Passo 2
Determine a média amostral das diferenças. A média é a soma de todos os valores dividido pelo número de valores.
Determine o desvio padrão da amostra das diferenças:
Determine o usando a tabela de distribuição de Student's T no apêndice com :
A margem de erro é:
Os limites do intervalo de confiança para são então:
Passo 3
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são as pontuações z na tabela de probabilidade normal do apêndice correspondente a uma área de (ou a área mais próxima) com (esses z-scores são dados em a tabela indicada).
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
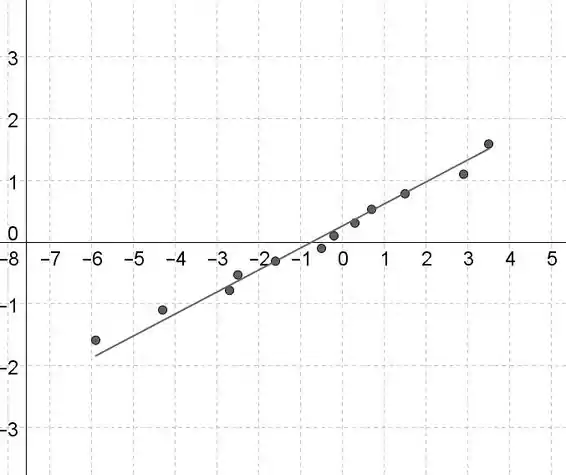
Se o padrão no gráfico de probabilidade normal é aproximadamente linear e não contém curvatura forte, então é apropriado assumir que a distribuição da população é aproximadamente normal.
O gráfico não contém curvatura forte e é aproximadamente linear, portanto, é plausível que as diferenças se originem de uma distribuição normal.
Assim, as suposições subjacentes à análise na parte (a) parecem ser satisfeitas.
Resposta
- Plausivelmente satisfeito