Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 2

Em uma amostra de 8 funcionários de uma empresa, observou-se duas variáveis: anos de empresa (A) e número de promoções recebidas (P). Com os resultados apresentados a seguir você diria que, para essa empresa, essas variáveis estão associadas?

Passo 1

Vamos montar a tabela de frequência conjunta dessas variáveis:

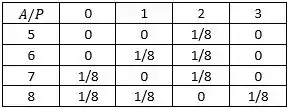
Passo 2

Temos uma amostra muito pequena e muito dispersa na tabela, todos os pares que tem alguma probabilidade associada a eles tem a mesma probabilidade, então é difícil perceber uma associação entre as variáveis, não dá para afirmar que 8 anos na empresa te garantem 2 ou 3 promoções, não posso nem afirmar que 8 anos de empresa te garantem pelo menos uma promoção, logo acredito que para essa pequena amostra, não parece plausível admitir que existe uma associação entre as variáveis.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam X 1 , … , X n vas independentes com valores médios μ 1 , … , μ n e variâncias σ 1 2 , … , σ n 2 . Considere uma função h x 1 , … , x n e use-a para definir uma nova va Y = h X 1 , … , X n . Sob

Uma aproximação mais precisa de E h X 1 , … , X n do Exercício 93 é h μ 1 , … , μ n + 1 2 σ 1 2 ∂ 2 h ∂ x 1 2 + ⋯ + 1 2 σ n 2 ∂ 2 h ∂ x n 2 Calcule-a para Y = h X 1 , X 2 , X 3 , X 4 , dado no Exercíc

a. X 1 tem distribuição qui-quadrado com parâmetro v 1 (veja a Seção 4.4), X 2 é independente de X 1 e tem uma distribuição qui-quadrado com parâmetro v 2 . Use a técnica do Exemplo 5.21 para mostrar

a. Use a fórmula geral da variância de uma combinação linear para escrever uma expressão para V ( a X + Y ) . Então, seja a = σ Y / σ X , e mostre que p ≥ - 1 . [Sugestão: a variância sempre é ≥ 0 , e

Se a quantidade de refrigerante que consumo em certo dia é independente do consumo em qualquer outro dia e é normalmente distribuída com μ = 13 oz e σ = 2 , e se eu atualmente tenho duas caixas com se