Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 1b
A tabela a seguir apresenta os valores observados em uma amostra de 130 empregados do ramo do comércio.
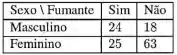
- Construa as tabelas marginais de frequência para as variáveis Sexo e Fumante.
- Se usássemos a amostra para tirar uma conclusão sobre toda a população, você diria que, proporcionalmente, mais homens fumam do que mulheres?
- Calcule o índice de associação entre as variáveis.
Passo 1
b) Se pudéssemos extrapolar as informações da amostra para toda a população, verificaríamos que sim, a proporção de fumantes entre os homens é maior do que dentre as mulheres, vamos verificar.
Passo 2
Na amostra temos um total de 42 homens, sendo 24 fumantes, logo
Dentro da amostra 57% dos homens são fumantes.
Passo 3
Enquanto que para as mulheres, temos um total de 88 mulheres e 25 fumantes:
Logo apenas 28% mulheres são fumantes nessa amostra.
Passo 4
Extrapolando esses dados para a população, realmente a proporção de homens fumantes na população é maior que a proporção de mulheres fumantes.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
a. Mostre que C o v X ,Y + Z = C o v X ,Y + C o v ( X ,Z ) . b. Sejam X 1 e X 2 as pontuações verbal e quantitativa em um exame de aptidão, e Y 1 e Y 2 as pontuações correspondentes em outro exame. Se
Suponha que a proporção de eleitores rurais em um determinado estado que favorece certo candidato a governador seja de 0,45 e que a proporção de eleitores urbanos e suburbanos que o favorecem seja de
Suponha que a pontuação verbal X e a pontuação quantitativa Y de um indivíduo escolhido aleatoriamente em um exame de aptidão administrado nacionalmente tenham fdp conjunta. f x , y = 2 5 2 x + 3 y0 ≤
Um aluno tem uma aula que supostamente termina às 9 h e outra que começa às 9h10. Suponha que a hora de término real da aula das 9 h seja uma va normalmente distribuída X 1 com média de 9h02 e desvio
Consulte o Exercício 58 e suponha que os X i s sejam independentes com cada um tendo distribuição normal. Qual é a probabilidade de o volume total embarcado ser de no máximo 100.000 pé3?