Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.2 - Ex. 5a

Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse experimento, associamos as variáveis aleatórias: número da bola retirada na caixa I (X), soma dos valores das duas bolas retiradas (Y) e a diferença, em módulo, desses valores (Z).

  1. Determine a função de probabilidade conjunta entre X e Y e entre Y e Z.
  2. Verifique se X e Y são independentes. Idem para Y e Z.
  3. Calcule a covariância entre X e Y.
  4. Obtenha V a r X + Y .

Passo 1

  1. A variável X pode assumir os valores 0,1 ,   já a variável Y por ser a soma dos valores das duas bolas retiradas, pode assumir os valores {-1, 0, 1}, vamos assumir que existe a probabilidade de ½ de se tirar uma bola qualquer de qualquer uma das duas caixas, e vamos pensar nos possíveis pares ( x , y ) existentes, logo:

P X = 0 , Y = - 1 = 1 2 × 1 2 = 1 4

P X = 0 ,   Y = 0 = 1 2 × 1 2 = 1 4

P X = 1 ,   Y = 0 = 1 2 × 1 2 = 1 4

P X = 1 ,   Y = 1 = 1 2 × 1 2 = 1 4

Passo 2

Montando a tabela conjunta de X / Y :

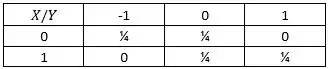
Passo 3

Para o par Y / Z , temos que Y pode assumir {-1, 0, 1} e que Z pode assumir {0, 1, 2}, os possíveis pares ( y ,   z ) são:

P Y = - 1 ,   Z = 1 = 1 4

P Y = 0 , Z = 0 = 1 4

P Y = 0 , Z = 2 = 1 4

P Y = 1 ,   X = 1 = 1 4

Passo 4

Montando a tabela conjunta Y / Z :

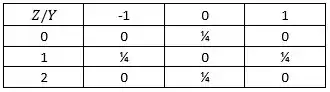
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ecologista deseja selecionar um ponto dentro de uma região circular de amostragem, de acordo com uma distribuição uniforme (na prática, isso poderia ser feito selecionando-se primeiro uma direção e
Na estimativa de custo, o preço total de um projeto é a soma dos gastos das tarefas componentes. Cada custo é uma variável aleatória com uma distribuição de probabilidade. É costume obter informações
Um restaurante serve três pratos ao preço fixo de US$ 12, US$ 15 e US$ 20. Para um casal selecionado aleatoriamente que janta nesse restaurante, sejam X custo do jantar do homem e Y custo do jantar da
Sejam A a porcentagem de um elemento de um espécime de rocha selecionado aleatoriamente, e B a porcentagem de um segundo elemento desse mesmo espécime. Suponha que D e E sejam erros de medição ao dete
Um espécime de rocha de uma área específica é selecionado aleatoriamente e pesado duas vezes. Represente por W o peso real e por X 1 e X 2 os dois pesos medidos. Então, X 1 = W + E 1 e X 2 = W + E 2 ,