Após um período de aprendizado, uma organização aplica um exame no qual o indivíduo deve ser aprovado a fim de ser elegível para se tornar sócio. Seja (aprovação de principiantes escolhidos aleatoriamente). A organização quer um exame que a maioria, mas não todos, consiga passar, de modo que decide que é desejável. Para um exame específico, as hipóteses relevantes são versus a alternativa . Suponha que dez pessoas façam o exame, e seja o número de aprovados.

a. A região de cauda inferior especifica um teste nível 0,01 ?

b. Mostre que, apesar de ser bicaudal, nenhum teste bicaudal é teste nível 0,01 .

c. Desenhe um gráfico de em função de para o teste. Isso é desejável?

Mostre que, apesar de ser bicaudal, nenhum teste bicaudal é teste nível 0,01

b. O primeiro valor a ser colocado na parte de cauda superior de uma região de duas caudas seria 10 , mas P(X=10 quando p=.9)=.349, então sempre que 10 estiver na região de rejeição, α≥.349 .

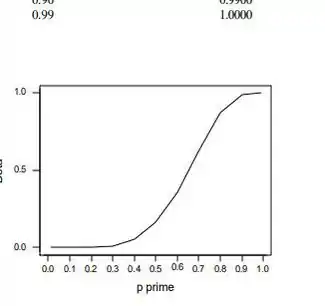
c. Usando a fórmula bicaudal para ß( na p. 341, calculamos o valor para o intervalo de valores p' possíveis. Os valores de que escolhemos, bem como o B( associado) estão na tabela abaixo, e o esboço a seguir. B( ) parece ser bastante grande para uma grande variedade de valores de .