Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 2.Exercícios - Ex. 99
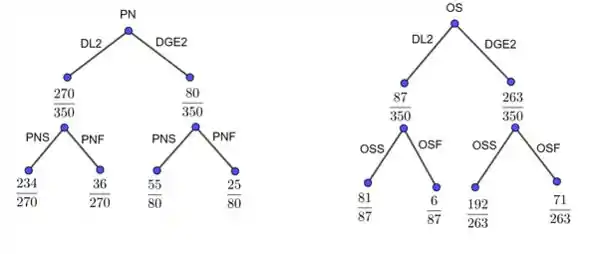
Um artigo na British Medical Journal “Comparison of treatment of renal calculi by operative surgery, percutaneous nephrolithotomy, and extracorporeal shock wave lithotripsy” - Comparação de tratamento de cálculo renal por cirurgia, por nefrolitotomia percutânea e por litotripsia com onda de choque - (1986, Vol.82, pág 879-892) forneceu a seguinte discussão de taxas de sucesso na remoção de pedras nos rins. Cirurgia aberta tem uma taxa de sucesso de 78% (273/350), enquanto um método mais novo, nefrolitotomia percutânea (NP), tem uma taxa de sucesso de 83% (289/350). Esse novo método pareceu melhor, mas os resultados mudaram quando o diâmetro da pedra foi considerado. Para pedras com diâmetros menores do que dois centímetros, 93% (81/87) de casos de cirurgia aberta obtiveram sucesso comparados com somente 83% (234/270) de casos de NP. Para pedras maiores do que ou iguais a dois centímetros, as taxas de sucesso foram 73% (192/263) e 69% (55/80) para cirurgia aberta e NP, respectivamente. Cirurgia aberta é melhor para ambos os tamanhos de pedra, porém tem menos sucesso no total. Em 1951, E. H. Simpson alertou para essa aparente contradição (conhecida como Paradoxo de Simpson), porém o risco ainda hoje persiste. Explique como a cirurgia aberta pode ser melhor para ambos os tamanhos de pedra, porém pior para o total.
Passo 1
Seja o evento que o diâmetro da pedra é menor que 2 cm.
Seja o evento em que o diâmetro da pedra é maior ou igual a 2 cm.
Seja o evento de que um caso de cirurgia aberta foi bem-sucedida.
Seja o evento que um caso de cirurgia aberta não foi bem-sucedida.
Seja o evento em que um caso do método PN foi bem-sucedido.
Seja o evento em que um caso do método PN não foi bem sucedido.
O problema pode ser descrito detalhadamente usando o seguinte diagrama em árvore:
Para cirurgia aberta, o número de casos com o diâmetro inferior a 2 cm é muito pequeno (87) comparado ao número de casos com o diâmetro maior que ou igual a 2 cm e a taxa de sucesso para diâmetros pequenos é muito maior que a taxa de sucesso para diâmetros grandes .
Para PN, o número de casos com diâmetro inferior a 2 cm é muito grande (270) comparado ao número de casos com diâmetro maior ou igual a 2 cm (80) e a taxa de sucesso para diâmetros pequenos é maior que a taxa de sucesso para diâmetros grandes .
Passo 2
A partir do diagrama temos:
Então,