Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 76
O artigo "Pine Needles as Sensors of Atmospheric Pollution" (Environ. Monitoring, 1982, p. 273-286) relatou o uso da análise da atividade do nêutron para determinar a concentração de poluentes nas agulhas de pinheiro. De acordo com os autores do artigo, "Essas observações indicaram fortemente que, para esses elementos determinados pelos procedimentos analíticos, a distribuição da concentração é lognormal. Portanto, nos testes de significância, os logaritmos das concentrações serão usados". Os dados fornecidos referem-se à concentração de bromina nas agulhas tiradas de um local próximo a uma usina de vapor a óleo queimado e de um local relativamente limpo. Os valores resumidos são médias e desvios padrão das observações logtransformadas.
- Seja *1 a média real do log da concentração no primeiro local, e defina *2 analogamente ao segundo local. a. Use o teste t combinado (assumindo normalidade e desvios padrão iguais) para decidir, no nível de significância 0,05, se as duas médias da distribuição da concentração são iguais
- Se *1 e *2, os desvios padrão das duas distribuições do log da concentração, não são iguais, 1 e 2, as médias das distribuições da concentração, seriam as mesmas se *1 *2 ? Explique o seu raciocínio.
Passo 1
- Reivindicação dada: Difere
- reivindicar: Difere
A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter uma igualdade.
Determine o desvio padrão combinado:
Determine a estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da tabela de distribuição t de Student no apêndice contendo o valor t na linha
Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Há evidências suficientes para rejeitar a alegação de que as duas médias de distribuição de concentração são iguais.
Passo 2
A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter uma igualdade.
Determine a estatística de teste:
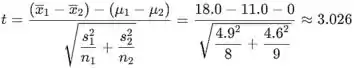
Determine os graus de liberdade (arredondados para o inteiro mais próximo):
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha df=14:
Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Há evidências suficientes para rejeitar a alegação de que as duas médias de distribuição de concentração são iguais.
Resposta
- Há evidência suficiente para rejeitar a alegação de que as duas médias de distribuição de concentração são iguais.
- Há evidência suficiente para rejeitar a alegação de que as duas médias de distribuição de concentração são iguais. Mesma conclusão