Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 45
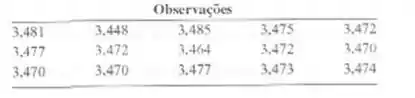
Um artigo na revista Technometries (1999, vol. 41. pp. 202-211) estudou a capacidade de um medidor de medição o peso de papel. Os dados para medidas repetidas de uma follna de papel sao mostrados na tabela a seguir. Construa um intervalo unilateral superior de confianca de 95% para o desvio-padrao dessas medidas. Veritique a suposicao de normalidade dos dados e comente sobrc as suposicos para o intervalo de confianga.
Passo 1
Vamos lá pessoal, se liga aqui como que resolve essa questão:
Um gráfico de probabilidade normal é um método gráfico para determinar se os dados da amostra estão em conformidade com uma distribuição normal hipotética com base em um exame visual subjetivo dos dados.
Para construir um gráfico de probabilidade, as observações na amostra são as primeiras classificados do menor ao maior. Ou seja, a amostra está organizado como onde é a menor observação, é a segunda menor observação e assim por diante com sendo a maior. A frequência cumulativa para observação em é:
Uma probabilidade normal é construída em eixos ordinários traçando as pontuações normais padronizadas contra onde as pontuações normais padronizadas satisfazem
Passo 2
Nos eixos horizontais estão os valores . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados desviarem significativamente da linha reta, o modelo hipotético não é apropriado.
Na forma descrita anteriormente, construímos um gráfico de probabilidade normal com base
nas observações
3,481 3,448 3,485 3,475 3,472 3,477 3,1172 3,464 3,472 3,470, 3.470, 3.470 3.477 3.473 3.474
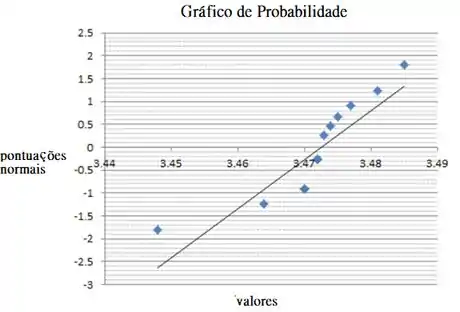
O gráfico de probabilidade normal não contém curvatura forte e o padrão é aproximadamente linear, então podemos concluir que os valores dos dados são aproximadamente normalmente distribuídos.
Passo 3
Se é a variância da amostra com tamanho n de uma variável aleatória de uma população normal com uma variância de , e um IC de para é:
Sabemos que tamanho simples n = 14, a média da amostra é
e o desvio padrão é:
O nível de confiança é de 95%, então
E, portanto:
Das equações, temos:
Então
Portanto, o intervalo de confiança superior unilateral de 95% para é