Headability é a habilidade de uma peça cilíndrica de material ser moldada na cabeça de um pino, parafuso ou outro item fabricado a frio sem rachar. O artigo "New Methods for Assessing Cold Heading Quality" (Wire J. Intl., out. 1996, p. 66-72) descreveu o resultado de um teste de impacto de headability aplicado a 30 espécimes de aço de alumínio neutralizado e a 30 espécimes de aço de silício neutralizado. A média amostral do número do grau de headability dos espécimes de aço foi 6,43, e a média amostral dos espécimes de alumínio foi 7,09. Suponha que os desvios padrão amostrais foram 1,08 e 1,19, respectivamente. Você concorda com os autores do artigo de que a diferença nos graus de headability é significativa no nível de 5% (assumindo que as duas distribuições de headability sejam normais)?
Passo 1
A suposição de que duas distribuições de cabebilidade são normais torna o teste tt de duas amostras o melhor para este caso.
Dadas duas distribuições normais, a variável aleatória (padronizada)
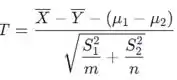
tem distribuição t de alunos aproximadamente com graus de liberdade , onde é

deve ser arredondado para o inteiro mais próximo.
O teste t de duas amostras para testar usa o seguinte valor da estatística de teste

Para a hipótese alternativa adequada a área adequada sob o curva é o valor de P.
Passo 2
As hipóteses de interesse são versus onde são a verdadeira classificação média de cabeçote para amostras de aço temperado com alumínio e a verdadeira média para aço temperado com silício, respectivamente. Para valores fornecidos
O valor da estatística t é
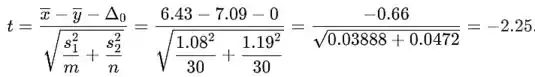
Passo 3
Para calcular o valor de P, você precisa calcular os graus de liberdade primeiro

e o inteiro arredondado para baixo mais próximo é 57, portanto
A hipótese alternativa é este valor de P é duas vezes a área sob o curva à direita de |t|. Desta forma
onde T é a estatística dos alunos com 57 graus de liberdade, e o valor foi calculado por um software (você poderia ter tirado o valor aproximado da tabela - estime-o).
O valor de P é
Então devemos rejeitar a hipótese nula. sim, você deve concordar com o autor do artigo.
Resposta
Então devemos rejeitar a hipótese nula. sim, você deve concordar com o autor do artigo.