Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 3.Exercícios - Ex. 75

Um artigo na revista Information Security Technical Report “Malicious software- past, present and future” - Programa Computacional Malicioso - passado, presente e futuro - (2004, Vol. 9. pp.6-18) forneceu os seguintes dados sobre os dez maiores casos de programas computacionais maliciosos de 2002. O líder claro no número de incidentes registrados no ano de 2002 foi “Klez”, worm internet, e ainda é uma das ameaças mais difundidas. Esse vírus foi primeiro detectado em 26 de outubro de 2002 e tem-se mantido por um período mais longo da história da virologia no topo entre os programas mais maliciosos.

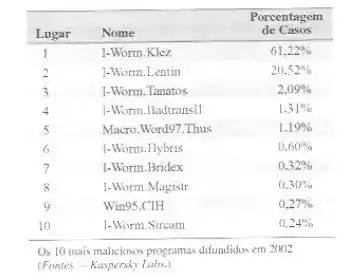
Suponha que 20 exemplos de programas maliciosos sejam reportados. Suponha que as fontes maliciosas possam ser consideradas independentes.

  1. Qual é a probabilidade de no mínimo um caso ser “Klez”?
  2. Qual é a probabilidade de três ou mais casos serem “Klez”?
  3. Quais são a média e o desvio-padrão do número de casos “Klez” entre os 20 reportados?

Passo 1

Seja X a variável aleatória do número de instâncias de Klez (do total de instâncias). X tem a distribuição binomial com os parâmetros a = 20 ,   p = 0.6122

A função de massa de probabilidade de X é dada por:

p ( X = k ) = C 20 k 0.612 2 k × 0.387 8 20 - k ,   k = 0,1 , . . .   , 20

Passo 2

Vamos calcular as letras usando essa fórmula:

Letra a:

P ( X ≥ 1 ) = 1 - P ( X = 0 )   ≈   1

Passo 3

Letra b:

P ( X ≥ 3 ) = 1 - P ( X = 0 ) - P ( X = 1 ) - P ( X = 2 )   ≈   0.999997

Passo 4

E na c, vamos calcular a média e o desvio padrão:

O valor esperado (ou médio) μ é a soma do produto de cada possibilidade x com sua probabilidade P ( x ) :

E ( X ) = n p = 20 × 0.6122 = 12.244

E o desvio padrão:

σ X = n p ( 1 - p ) = 2.179

Resposta

  1. 1
  2. 0.999997
  3. m é d i a :   12.244 ,   d e s v i o - p a d r ã o :   2.179
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A variável aleatória X tem uma distribuição binomial, com n=10 e p=0.5 . Esquematize a função de probabilidade de X.Qual é o valor mais provável de X?Qual(is) é(são) o(s) valor(es) menos provável(is)
De um lote que contém 25 peças, das quais 5 são defeituosas, são escolhidas 4 ao acaso. Seja X o número de defeituosas encontradas. Estabeleça a distribuição de probabilidades de X quandoa) As peças f
Suponha que a variável aleatória X tenha os valores possíveis 1 , 2 , 3 , ..., e P X = j = 1 2 j , j = 1 , 2 , ...a) Calcule P Xs e rp a r .b) Calcule P X ≥ 5 .c) Calcule P Xs e rd i v i s í v e lp o
Sabe-se que uma determinada moeda apresenta cara três vezes mais frequentemente que coroa. Essa moeda é jogada três vezes. Seja X o número de caras que aparece. Estabeleça a distribuição de probabilid
Uma máquina impressora pode imprimir n letras, digamos α 1 ,α 2 ,… α n . Ela é acionada por impulsos elétricos, cada letra sendo produzida por um impulso diferente. Suponha que exista uma probabilidad