Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 3.Exercícios - Ex. 66
A variável aleatória X tem uma distribuição binomial, com n=10 e p=0.5 . Esquematize a função de probabilidade de X.
- Qual é o valor mais provável de X?
- Qual(is) é(são) o(s) valor(es) menos provável(is) de X?
Passo 1
Temos os seguintes dados:
A definição de probabilidade binomial é o seguinte:
Vamos avaliar em :
Passo 2
Agora vamos repetir para e chegar nessa tabela aqui:
Vamos aproveitar também para fazer o gráfico
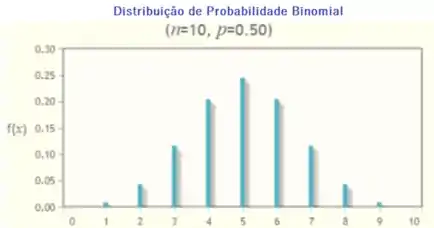
Passo 3
Letra a:
O valor de 5 é o mais provável, porque tem a maior probabilidade na tabela.
Passo 4
Letra b:
O valor de 0 e 10 é o menos provável, porque e tem a menor probabilidade de 0,001 na tabela.
Resposta
- 5
- 0 e 10
Exercícios de Livros Relacionados
Sabe-se que os parafusos produzidos por uma certa companhia são defeituosos com probabilidade 0,01, independentemente uns dos outros (isto é, a fração não=conforme de parafusos na produção é 0,01). A
Uma moeda, cuja probabilidade de cara em um lançamento é p ,0p1 , é lançada indefinidamente até que ocorra uma sequência de cinco caras (seguidas). Um estudante resolve modelar esse experimento defini
Sabe-se que a porcentagem de vitórias para que o time de basquete da NBA Chicago Bulls fosse para as finais das temporadas de 1996-97 era de 87,7. Arredonde-a para 90 para usar a Tabela A. 1.(a) Qual
No Exercício 5-9, quantos dos 15 caminhões vocês esperaria que tivessem pneus furados? De acordo com o teorema de Chebyshev, há uma probabilidade de pelo menos 3/4 de que o número de caminhões com pne
Um engenheiro de controle de tráfego relata que 75% dos veículos que passam por um ponto de checagem são do estado. Qual é a probabilidade de que menos de quatro dos próximos nove veículos sejam de fo