Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 86
No artigo que serve de referência no Exercício 85, havia realmente quatro tratamentos experimentais: não-diabético de controle, diabético não-tratado, diabético de dose baixa e diabético de dose alta. Represente o tamanho da amostra do i-ésimo tratamento por ni e a variância amostral por (i = 1, 2, 3, 4). Assumindo que a variância real de cada tratamento é 2 , construa um estimador combinado de 2 que seja não-tendencioso e verifique o uso das regras do valor esperado que é, de fato, não-tendencioso. Qual é sua estimativa para os dados reais a seguir? (Sugestão: modifique o estimador combinado na pág. 328.)
Passo 1
- Dado:
- Determine a diferença de valor de cada par.
- Os arremessadores parecem ter maior diferença na translação ântero-posterior lateral de seus ombros em comparação com os jogadores de posição, porque o intervalo de confiança na parte (a) está completamente acima do intervalo de confiança na parte (b)
Determine a diferença de valor de cada par.
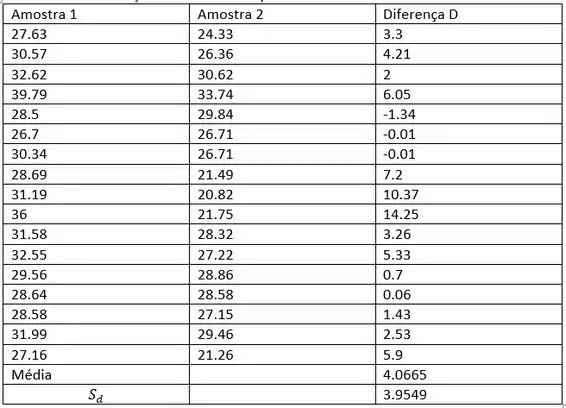
Passo 2
Determine a média amostral das diferenças. A média é a soma de todos os valores dividido pelo número de valores.
Determine o desvio padrão da amostra das diferenças:
Determine o usando a tabela de distribuição de Student's T no apêndice com df=n-1=17-1=16:
A margem de erro é então:
Os pontos finais do intervalo de confiança para são:
Estamos 95% confiantes de que a verdadeira diferença média na tradução entre os braços dominantes e não dominantes para arremessadores está entre 2.0330 e 6.1000
Passo 3
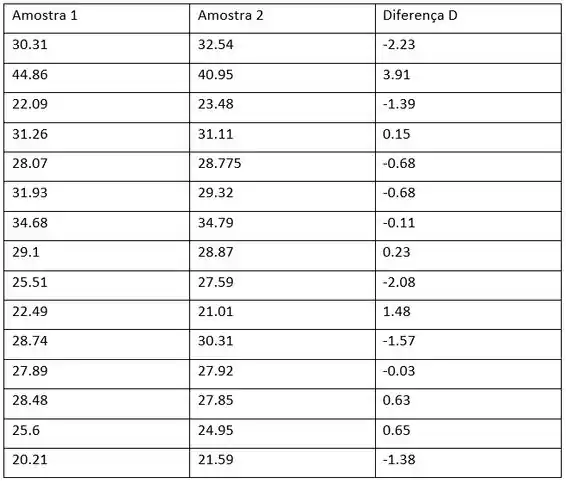
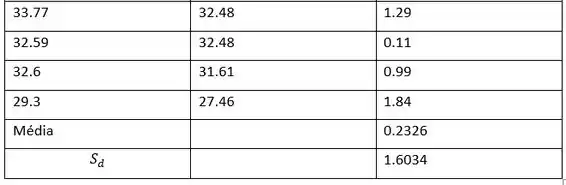
Determine a média amostral das diferenças. A média é a soma de todos os valores dividido pelo número de valores.
Determine o desvio padrão da amostra das diferenças:
Determine o usando a tabela de distribuição T de Student no apêndice com :
A margem de erro é então:
Os pontos finais do intervalo de confiança para são:
Estamos 95% confiantes de que a verdadeira diferença média na tradução entre os braços dominantes e não dominantes para jogadores de posição está entre -0.5402 e 1.0054
Resposta
- Os arremessadores parecem ter maior diferença na translação ântero-posterior de seus ombros de lado a lado em comparação com os jogadores de posição