Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 66
Os autores do artigo "Dynamics of Canopy Structure and Light Interception in Pinus elliotti, North Florida" (Ecological Monographs, 1991, p. 33-51) planejaram um experimento para determinar o efeito de fertilizantes em uma medida de área plantada. Diversos gráficos estavam disponíveis para o estudo e metade foi selecionada aleatoriamente para ser fertilizada. Para garantir que os quadros que receberiam o fertilizante e os quadros de controle fossem semelhantes, antes de começar o experimento, a densidade de árvores (o número de árvores por hectare) foi registrada para oito quadros a serem fertilizados e para oito quadros de controle, resultando nos dados fornecidos. A saída do MINITAB é exposta a seguir.
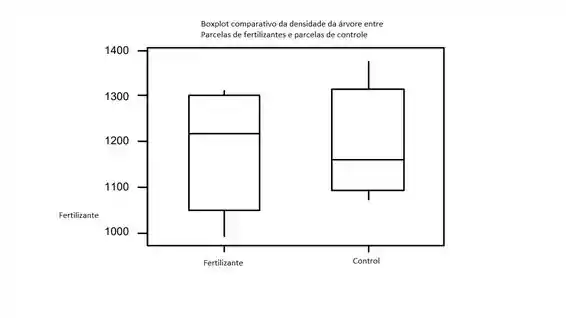
a. Construa um boxplot comparativo e comente sobre quaisquer características interessantes. b. Você concluiria que há uma diferença significativa na densidade média de árvores dos quadros fertilizados e de controle? Use 0,05. c. Interprete o intervalo de confiança dado.
Passo 1
- Um teste de vs produz um valor t de -0,20 e um valor p de duas caudas de 0,85. (d.f. = 13). Nós falharíamos em rejeitar ; os dados não indicam uma diferença significativa nas médias.
- Com 95% de confiança podemos dizer que a verdadeira diferença média entre a densidade da árvore das parcelas de fertilizantes e a das parcelas de controle está em algum lugar entre –144 e 120. Como esse intervalo contém 0, 0 é um valor plausível para a diferença, que suporta a conclusão com base no valor de p.
Embora a mediana da parcela de fertilizantes seja maior do que a das parcelas de controle, a os dados da parcela de fertilizantes parecem distorcidos negativamente, enquanto o oposto é verdadeiro para o controle dados de plotagem
Passo 2
Resposta
Ver o desenvolvimento.