Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 59
A rigidez e a fibrosidade do aspargo são os principais determinantes de sua qualidade. Esse foi o objeto de estudo relatado em “Post–Harvest Glyphosphate Appliction Reduces Toughening, Fiber Content, and Lignification of Stored Asparagus Spears” (J. of the Amer. Soc. of Horticultural Science, 1988, p. 569–572). Esse artigo relatou os dados a seguir (reproduzidos de um gráfico) sobre x força de corte (kg) e y porcentagem do peso seco da fibra
a. Calcule o valor do coeficiente de correlação amostral. Com base nesse valor, como você descreveria a natureza da relação entre as duas variáveis? b. Se uma primeira amostra tiver um valor maior de força de corte do que uma segunda amostra, que porcentagem do peso seco da fibra tende a ser real para as duas amostras? c. Se a força de corte for expressa em libras, o que acontecerá ao valor de r? Por quê? d. Se o modelo de regressão linear simples fosse ajustado a esses dados, que proporção da variação observada na porcentagem do peso seco da fibra pode ser explicada pela relação do modelo? e. Faça um teste no nível de significância 0,01 para verificar se existe uma associação linear positiva entre as duas variáveis.
Passo 1
- O coeficiente de correlação da amostra r é dado por
- Conforme concluído em (a), a correlação é positiva, o que significa que a maior força de cisalhamento resulta em maior porcentagem de peso de fibra seca
- Por causa da definição de r
- A relação entre o coeficiente de correlação da amostra e o coeficiente de determinação é dada por
- Ao testar versus uma das alternativas, a estatística de teste é
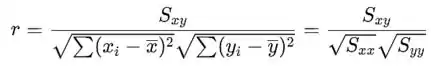
Onde
Calcule todos os valores necessários. As somas são dadas no exercício. O é
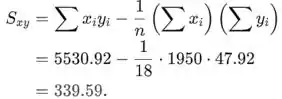
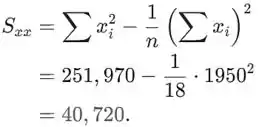
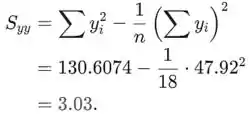
O coeficiente de correlação da amostra r é
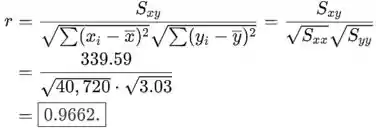
O r está próximo de 1, o que indica que há forte e positiva correlação entre a força de cisalhamento e o percentual de peso seco da fibra.
.
Passo 2
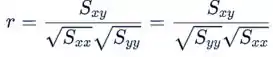
não importa como você rotula as variáveis - o coeficiente de correlação da amostra permaneceria o mesmo.
assim, o coeficiente de determinação, ou a proporção de variação observada é
Passo 3
que tem distribuição t com n-2 graus de liberdade, onde R é o coeficiente de correlação amostral como variável aleatória. Dependendo da hipótese alternativa, o valor de P é a área correspondente sob curva.
A hipótese alternativa é . O valor da estatística T é
O valor de P pode ser calculado usando software e é
Porque
rejeitar a hipótese nula em qualquer nível de significância razoável e concluir que as variáveis estão positivamente relacionadas linearmente
Resposta
- r = 0,923r=0,923;
- A maior força de cisalhamento resulta em maior percentual de peso de fibra seca;
- O coeficiente de correlação amostral permaneceria o mesmo;
- ; e. As variáveis estão positivamente relacionadas linearmente.