Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.2 - Ex. 1
Para se avaliar o nível de tensão ocasionada por exames escolares, doze alunos foram escolhidos e sua pulsação medida antes e depois do exame.
Faça um teste, com nível de significância de , para verificar se existe maior tensão (isto é, maior pulsação) antes da realização dos exames. Indique as suposições necessárias.
Passo 1
Antes de mais nada é extremamente importante que você consiga perceber que se trata de um teste pareado; isso porque para cada estudante, foram realizadas duas medições; de uma forma geral, sempre que tiver exercícios de antes e depois de alguma ação, busque sempre notar se as medições são feitas sobre uma mesma amostra.
Beleza creuza, que fazemos agora então?! Calma lá ó, primeiro toda vez que falarmos em teste pareado precisa vir na sua cabeça que vamos ter de tomar a diferença das duas medições.
Mas peraí, vamos definir quem estamos estudando:
Agora podemos começar calculando a diferença entre os valores:
Teremos a seguinte configuração:
Levando em consideração todos os sinais, devemos obter a média DAS DIFERENÇAS:
E a variância das diferenças:
Beleza, agora se considerarmos que essa diferença segue um modelo de distribuição Normal e que haja independência entre os estudantes, para realizar o teste a gente utiliza a seguinte aproximação pela t-student:
Passo 2
Vamos então definir quem raios são as hipóteses do teste:
Mas porque escolhemos assim? Veja bem, queremos testar se a tensão (pulsação) é maior ANTES da prova e como definimos nossa diferença como sendo então queremos testar se essa diferença é MAIOR do que zero. Ficou claro??
Se você optar por definir: , a sua hipótese alternativa deverá ser ; Capith?
Se estivermos entendidos, vamos agora definir a nossa região crítica:
O enunciado forneceu , portanto devemos buscar na tabela de t-student um valor tal que:
Mas, se você lembrar bem, a tabela de t-student, fornece colunas com valores , que é definido de acordo com a região crítica. COMO ASSIM? ó:
Se RC BILATERAL, isto é, com sinal de nos obriga a uma região crítica do tipo , lembrou? Para esse caso teremos:
E quando tivermos uma RC UNILATERAL, que se da quando a hipótese alternativa apresenta sinal de menor ou maior, temos:
Foi? Com isso, para obtermos o valor de vamos ter de ir na coluna que representa
E na linha de graus de liberdade.
Vai lá, da uma procurada, depois volta aqui pra conferir!
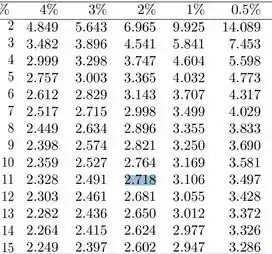
Achou a mesma coisa que eu aí??
Portanto:
Passo 3
Por último, precisamos realizar o teste:
Uia! Foi por pouco; mas não pertence à região crítica, então devemos aceitar a hipótese nula.
Resposta
Concluindo essa bagaça, encontramos evidências de que as tensões dos alunos, antes e depois da prova, são as mesmas.