Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.2 - Ex. 4
As variáveis seguem a distribuição Normal com mesma variância. Deseja-se testar se, também, têm a mesma média. Doze observações de cada variável foram escolhidas e os resultados foram os seguintes:
Qual é a conclusão ao nível de significância de 5%?
Passo 1
Seguimos, mais uma vez temos um teste para a média de duas populações só que dessa vez temos variâncias populacionais desconhecidas e IGUAIS.
Portanto teremos de usar a seguinte aproximação:
Calma! Que diaxo é aquele ??
Então, ele nada mais é do que uma combinação das variâncias, veja só:
Tranquilo?!
Passo 2
Agora, precisamos usar os dados do enunciado para encontrar as médias e variâncias amostrais:
E
Agora as variâncias:
E
Ufa! Cansamo já! Mas carmeia que ainda falta um negocinho:
Agora sim! Falta pouco, vamos definir nossas hipóteses:
E nossa região crítica será:
Da tabela de t-student sabemos que quando nossa RC é bilateral:
Ou seja, precisamos buscar na tabela, um valor tal que:
Mas, lembre-se sempre de que as colunas tabela nos fornecem valores de ; e que quando nossa região crítica for BILATERAL:
Passo 3
No final das contas, precisamos ir na coluna de e buscar a intersecção com a linha de graus de liberdade:
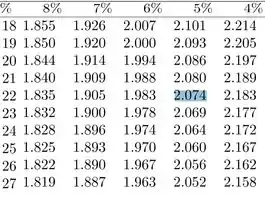
Encontramos então:
Portanto a nossa região crítica será dada por:
Finalmente podemos realizar o teste sob :
Concluimos que não pertence à nossa região crítica; portanto devemos ACEITAR .
Resposta
Então, existem evidências de que as médias das populações sejam iguais.