Para verificar se duas populações têm a mesma média, amostras independentes foram retiradas. Sabendo que a população é Normal (e a população Normal com , que conclusão pode ser tirada, ao nível de 2%? Os valores obtidos foram:

Agora, vamos definir quem serão nossas hipóteses:

Um último passo antes de realizar o teste, precisamos definir nossa região crítica:

Trata-se de uma RC bilateral, certo? Isso acontece porque nossa hipótese alternativa apresenta o sinal de ; então temos que sempre prestar atenção nela.

Voce deve se lembrar também que a tabela de distribuição Normal nos da valores para os quais:

Lembra? Isso ocorre porque o gráfico apresenta simetria.

Mas então precisamos buscar na tabela um valor , tal que:

Mas não se esqueça de que a tabela nos fornece valores de:

Portanto,

Vamos ter de buscar no corpo da tabela um valor próximo de 0,49:

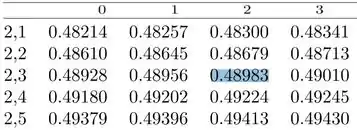
Ou seja, encontramos:

Então:

Isso nos deixa com uma região crítica com a seguinte forma:

Bem tranquilo, né?! Agora só falta realizar o teste, lembrando que a gente sempre realiza o teste “sob” , porque é ele quem apresenta o sinal de igual e então podemos substituir:

Perceba então que não pertence à nossa região crítica; devemos portanto aceitar .