Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.2 - Ex. 5
Para comparar as médias de duas populações Normais, amostras aleatórias foram obtidas. Sabe-se que as variâncias populacionais são diferentes, sendo seus valores desconhecidos.
O que pode ser dito a respeito das médias das populações, com ?
Passo 1
Oi Deus, sou eu denovo...
Mais um teste de comparação entre as médias com variâncias desconhecidas, só que dessa vez elas são ditas DIFERENTES.
Para esse caso então, vamos utilizar a seguinte aproximação:
O único diferencial dessa aproximação é aquele ali; temos que calcular ele da seguinte maneira:
Pois é, eu me perdi só de escrever aquilo ali.
Para seguirmos vamos ter de calcular ainda, as médias e variâncias amostrais:
E
Agora as variâncias:
E
E agora o :
Pay attention agora, toda vez que for um número quebrado, SEMPRE vamos arredondar para o MENOR inteiro mais próximo.
Ou seja, vamos usar graus de liberdade.
Passo 2
Se você tiver aqui ainda, vamos definir quem são as nossas hipóteses:
E um último passo antes de finalmente realizarmos o diaxo do teste; precisamos saber quem é a nossa região crítica tomando :
Ou seja, precisamos buscar na tabela de t-student um valor tal que:
Mas as colunas da tabela só nos dão valores , portanto quando tivermos uma RC BILATERAL, devemos tomar:
OBS: é muito importante saber essa diferença que ocorre quando RC for unilateral ou bilateral; lembrando que quando RC for UNILATERAL teremos .
OU seja, basta irmos na coluna que representa 5% e na linha de graus de liberdade:
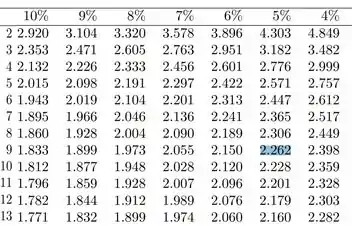
Chegamos no seguinte:
Portanto nossa RC:
Passo 3
Finalmente agora podemos realizar o teste sob :
Encontramos um que não pertence a nossa região crítica, portanto devemos ACEITAR a hipótese nula .
Resposta
Concluimos, que existem evidências de que as médias das populações sejam iguais.