Uma caixa contém 60 bolas verdes e 40 pretas. Retiram-se da caixa dois conjuntos de 30 bolas cada um, com reposição, e anotam-se suas cores. Qual é a probabilidade dos dois conjuntos diferirem de 8 ou mais bolas verdes?

Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.

Se a amostra for suficientemente grande, pode-se aproximar a Binomial por uma Normal de mesma média e mesma variância (na prática, para efeito dessa aproximação devemos considerar: e , ou ainda, para próximo de , se ), isto é:

Pelo enunciado temos os seguintes dados:

• ;
• ;
• ;
• ;
• .

E queremos saber a probabilidade dos dois conjuntos diferirem de 8 ou mais bolas verdes:

Então:

Pela tabela da distribuição normal é:

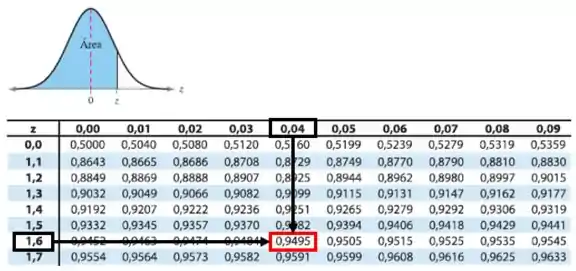
Tchau galerinha! Te espero em mais exercícios.