Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 8b
Determinar a probabilidade de, em 120 lances de uma moeda honesta, ocorrerem caras:
- em 5/8 ou mais.
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.
Ao retirar uma amostra aleatória de uma população, cada valor da amostra constitui uma variável aleatória cuja distribuição de probabilidades é a mesma da população no instante da retirada desse elemento para a amostra.
A distribuição amostral da proporção é quando temos uma população infinita (), com a probabilidade de sucesso () de um certo evento e de insucesso ().
Se a amostra for suficientemente grande, pode-se aproximar a Binomial por uma Normal de mesma média e mesma variância (na prática, para efeito dessa aproximação devemos considerar: e , ou ainda, para próximo de , se ), isto é:
Pelo enunciado temos os seguintes dados:
- ;
- ;
- .
E queremos saber a probabilidade de ocorrem caras em 5/8 ou mais, ou seja:
Passo 2
Então para :
Pela Tabela da Distribuição normal, temos:
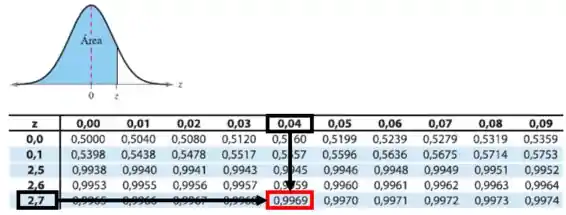
Pela figura presente na tabela, podemos observar que o valor obtido é para valores menores que 5/8:
Passo 3
Para valor em 5/8 ou mais:
Então a probabilidade de, em 120 lances de uma moeda honesta, ocorrerem caras em 5/8 ou mais:
Tchau galerinha! Te espero em mais exercícios.
Resposta
.