Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 25
De uma caixa que contém quatro moedas de 10 centavos e duas de 5 centavos, três moedas são selecionadas aleatoriamente sem reposição. Determine a distribuição de probabilidade para a soma dos valores das três moedas. Expresse a distribuição de probabilidade graficamente, por meio de um histograma de probabilidade.
Passo 1
Falaa, meu querido/minha querida. Vamos usar para representar o valor total das moedas selecionadas.
A variável pode assumir 3 valores diferentes:
Se as 3 moedas de 10 centavos são selecionadas: .
Se 2 moedas de 10 centavos e 1 de 5 centavos são selecionadas: .
Se 1 moeda de 10 centavos e 2 de 5 centavos são selecionadas: .
Como existem apenas 2 moedas de 5 centavos, é impossível selecionar 3 delas.
O número total de maneiras que as moedas podem ser selecionadas é:
Então, bora para os cálculos!!
Passo 2
Nós temos quando 3 moedas de 10 centavos são selecionadas, que pode ser descrito:
Então, a probabilidade é:
Passo 3
Nós temos quando 2 moedas de 10 centavos e 1 de 5 centavos são selecionadas, que pode ser descrito:
Então, a probabilidade é:
Passo 4
Nós temos quando 1 moeda de 10 centavos e 2 de 5 centavos são selecionadas, que pode ser descrito:
Então, a probabilidade é:
Passo 5
Sendo assim, nós temos que a distribuição de probabilidade é:
E o gráfico é descrito pela imagem abaixo:
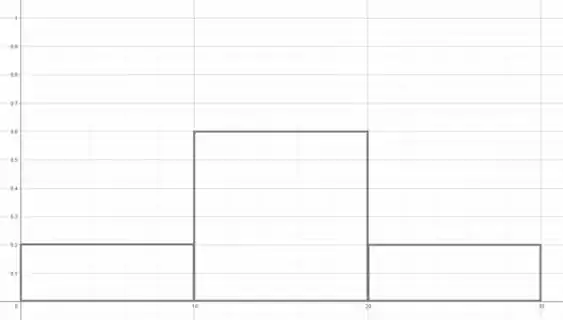
Resposta
Resolução nos passos anteriores.