Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios Suplementares - Ex. 75
Um restaurante serve três pratos ao preço fixo de US$ 12, US$ 15 e US$ 20. Para um casal selecionado aleatoriamente que janta nesse restaurante, sejam custo do jantar do homem e custo do jantar da mulher. A fmp conjunta de e é dada na tabela a seguir:
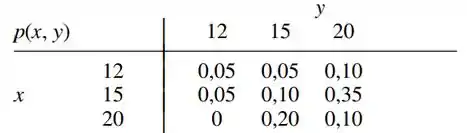
a. Calcule as fmps marginais de e .
b. Qual é a probabilidade de o jantar do homem e da mulher custar no máximo US$ 15 cada?
c. e são independentes? Justifique sua resposta.
d. Qual é o custo total esperado do jantar para as duas pessoas?
e. Suponha que, quando um casal abre biscoitos da sorte no final da refeição, encontra a mensagem “Vocês receberão de volta a diferença entre o custo da refeição mais cara e o da mais barata que escolheram”. Quanto o restaurante espera devolver?
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Para resolvermos esse exercício basicamente vamos precisar ver os valores correspondentes na tabela do enunciado e achamos a solução. Bora lá!!!
Passo 2
A fdc marginal de são os totais de linha da tabela fornecida:
E a fdc marginal de é:
Passo 3
A probabilidade de que ambos custem no máximo US$ 15 é:
Passo 4
As variáveis e não são independentes, porque as linhas da tabela do enunciado não contêm os mesmos valores.
Passo 5
O custo total do jantar é a soma do custo de cada jantar, logo .
O valor esperado é a soma do produto de cada possibilidade com sua probabilidade :
Logo, o total esperado é US$ 33,35.
Passo 6
A devolução é a dirença entre a média mais cara e média menos cara, então .
O valor esperado é calculado de forma similar ao Passo 5.
Portanto, o reembolso esperado é de US$ 3,85.
Resposta
Resolução nos passos anteriores.