Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 17a

Certas válvulas produzidas por uma empresa têm vida média de 900 h e desvio padrão de 80 h. A empresa envia 1.000 lotes, de 100 válvulas cada um. Em quantos lotes pode-se esperar que:

  1. a vida média exceda a 910 h?

Passo 1

Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.

Uma variável aleatória, obtida pela combinação linear de variáveis aleatórias normais independentes, tem também distribuição normal. Se a distribuição da população for normal, a distribuição amostral de X - também será normal, para qualquer tamanho de amostra. A figura a seguir representa um caso genérico, envolvendo a distribuição amostral de X - , no caso de população normal.

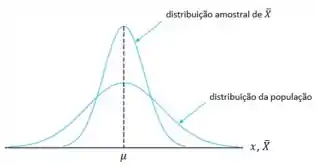
Podemos observar que quanto maior o tamanho n da amostra, menor será a variância de X - .

A variável normal padronizada da variável X - é:

z = X - - μ σ n

Pelo enunciado temos os seguintes dados:

  • μ = 900 ;
  • σ = 80 ;
  • n = 100 .

E queremos saber em quantos lotes pode-se esperar que a vida média exceda a 910 h, ou seja:

P X > 910

Passo 2

Então primeiramente iremos calcular z :

z = 910 - 900 80 100 = 1,25

Pela tabela da distribuição normal é:

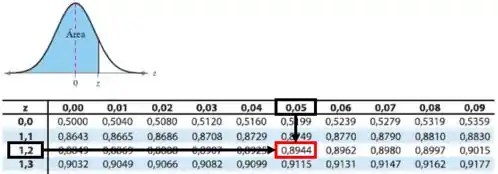
Pela tabela encontramos o valor de P X < 910 , então iremos subtrair de 1:

P X > 910 = 1 - P X < 910 = 1 - 0,8944 = 0,1056

Para 1000 lotes:

0,1056 ∙ 1000 = 106   l o t e s

Tchau galerinha! Te espero em mais exercícios.

Resposta

106   l o t e s .

Exercícios de Livros Relacionados

Determinar os pontos da distribuição qui-quadrado de modo que a área subtendida entre eles seja igual a 0,95, sendo ϕ = 20 , admitindo-se que as áreas laterais a esses pontos sejam iguais.
Uma urna contém 80 talões numerados, dos quais 60% são pares e 40% são ímpares. Entre 50 amostras, de 20 talões cada, selecionadas de urna, quantas amostras pode-se esperar que sejam constituídas:de n
Determinar X_(0,95)^2 para os graus de liberdade:
No exercício anterior, se a vida mediana é de 900 h, em quantos lotes pode-se esperar que a vida mediana exceda a 910 h?
Seja X 1 uma variável que representa qualquer dos elementos da população: 3, 7 e 8, e X 2 que representa qualquer dos elementos da população: 2 e 4. Calcular: