Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 18
No exercício anterior, se a vida mediana é de 900 h, em quantos lotes pode-se esperar que a vida mediana exceda a 910 h?
Passo 1
Oie, vem comigo! Do exercício 17, temos os seguintes dados:
- ;
- ;
- .
A variável normal padronizada da variável é calculada por:
Para o nosso exercício, sabemos que:
E queremos saber em quantos lotes pode-se esperar que a vida mediada exceda a 910 h, ou seja:
Para a distribuição por amostragem da mediana , podemos utilizar as equações:
Passo 2
Calculando a variância para a mediada:
Agora conseguimos calcular o valor de :
Pela tabela da distribuição normal é:
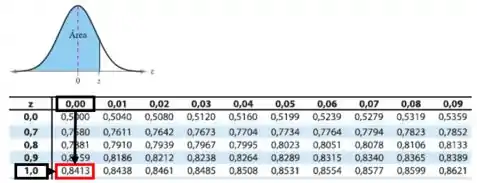
Pela tabela encontramos o valor de , então iremos subtrair de 1:
Para 1000 lotes:
Até mais pessoal!
Resposta
.
Exercícios de Livros Relacionados
Um fabricante faz a remessa de 1.000 lotes, de 100 parafusos cada um. Se 5% dos parafusos são normalmente defeituosos, em quantos lotes pode-se esperar que existam:menos que 90 parafusos perfeitos;98
Se a variável X apresenta uma distribuição de Student com ϕ = 10 , determinar a constante K de modo que:
Certas válvulas produzidas por uma empresa têm vida média de 900 h e desvio padrão de 80 h. A empresa envia 1.000 lotes, de 100 válvulas cada um. Em quantos lotes pode-se esperar que:a vida média exce
Uma caixa contém 60 bolas verdes e 40 pretas. Retiram-se da caixa dois conjuntos de 30 bolas cada um, com reposição, e anotam-se suas cores. Qual é a probabilidade dos dois conjuntos diferirem de 8 ou
Os relês fabricados pela empresa A têm duração média de 1.400 h e desvio padrão de 200h, enquanto que os da empresa B têm duração média de 1.200 h e desvio padrão de 100h. Se forem ensaiadas amostras