Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 13

Seja X 1 uma variável que representa qualquer dos elementos da população: 3, 7 e 8, e X 2 que representa qualquer dos elementos da população: 2 e 4. Calcular:

Passo 1

Oi galerinha, vem comigo pra gente entender este exercício juntos!

Seja X é uma população de média μ e variância σ 2 , na qual se extrai uma amostra aleatória de n elementos. Sabe-se que:

μ = ∑ X i n

σ 2 = ∑ ( X i - μ ) 2 n

Pelo nosso enunciado temos que:

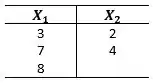
Então a média populacional de X 1 e X 2 , respectivamente:

μ   ( X 1 ) = 3 + 7 + 8 3 = 6

μ   X 2 = 2 + 4 2 = 3

Passo 2

A média da distribuição amostral das diferenças ou somas é dada pela seguinte equação:

μ   X 1 ± X 2 =   μ   X 1 ± μ   X 2

Como no nosso exercício queremos saber a diferença entre as médias, temos o seguinte:

μ   X 1 - X 2 =   μ   X 1 - μ   X 2 = 6 - 3 = 3

Passo 3

O desvio padrão populacional para X 1 e X 2 , respectivamente:

σ   X 1 = 3 - 6 2 + 7 - 6 2 + 8 - 6 2 3 = 2,16

σ   X 2 = 2 - 3 2 + 4 - 3 2 2 = 1,00

Passo 4

A variância da distribuição amostral das diferenças ou somas, será sempre a soma das variâncias:

σ 2   X 1 ± X 2 = σ 2   X 1 + σ 2   X 2

Então, para o desvio padrão, temos o seguinte:

σ   X 1 - X 2 = σ 2   X 1 + σ 2   X 2 = ( 2,16 ) 2 + ( 1,00 ) 2  

σ   X 1 - X 2 = 2,38

Tchau galerinha! Te espero em mais exercícios.

Resposta

  1. μ   ( X 1 ) = 6 .
  2. μ   X 2 = 3 .
  3. μ   X 1 - X 2 = 3 .
  4. σ   X 1 = 2,16 .
  5. σ   X 2 = 1,00 .
  6. σ   X 1 - X 2 = 2,38 .

Exercícios de Livros Relacionados

Uma pesquisa de opinião pública numa comunidade mostrou que 46% das pessoas são favoráveis a um projeto de lei. Determinar a probabilidade de que a maioria das pessoas, de um conjunto amostral de 1.00
Determinar os valores críticos de X 2 para os quais a área da extremidade direita da distribuição Qui-Quadrado será 5%, quando o número de graus de liberdade for de:
A e B jogam uma partida de “cara e coroa”, lançando cada um 50 moedas. A vencerá o jogo se conseguir 5 ou mais caras do que B e, quando isso não ocorrer, B vencerá. Determinar as vantagens contra a vi
Determinar os pontos da distribuição qui-quadrado de modo que a área subtendida entre eles seja igual a 0,95, sendo ϕ = 20 , admitindo-se que as áreas laterais a esses pontos sejam iguais.
Uma urna contém 80 talões numerados, dos quais 60% são pares e 40% são ímpares. Entre 50 amostras, de 20 talões cada, selecionadas de urna, quantas amostras pode-se esperar que sejam constituídas:de n