Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 2.2 - Ex. 5
Comente a afirmação: se dois eventos são mutuamente exclusivos então eles não são independentes.
Passo 1
Oi, tudo bem? Bora resolver esse exercício?
Para facilitar, vamos supor dois eventos mutuamente exclusivos. Dado um lançamento de um dado considere os eventos E , conforme é ilustrado a seguir:
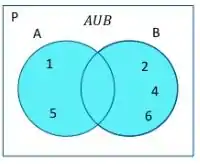
Devemos responder, será que eles não são independentes?
Passo 2
Observe que ,
Para que os eventos sejam independentes, devemos ter que
Mas,
Ou seja, eles não são independentes.
Resposta
Logo, podemos concluir que a afirmação é válida para eventos diferentes de vazio, poi se um desses fosse, teríamos que sempre
Exercícios de Livros Relacionados
Diz-se que o evento F carrega informações negativas a respeito do evento E, e escrevemos F ↘ E , se: P E F ≤ P ( E ) Demonstre ou dê contraexemplos para as seguintes afirmativas:(a) Se F ↘ E ,então E
Se você tivesse que construir um modelo matemático para os eventos E e F descritos nas letras (a) até (e) a seguir, você os consideraria eventos independentes? Explique o seu raciocínio.(a) E é o even
Suponha que queiramos gerar o resultado da jogada de uma moeda honesta, mas que tudo o que tenhamos a nossa disposição seja uma moeda viciada que dá cara com alguma probabilidade desconhecida p difere
Realizam-se jogadas independentes de uma moeda que dá cara com probabilidade p. Supondo que H e T representem os eventos "cara" e "coroa”, qual é a probabilidade de que os primeiros quatro resultados
Uma questão de verdadeiro ou falso é colocada para um time formado por um marido e sua esposa em um jogo de perguntas e respostas. Tanto o homem quanto a mulher darão, de forma independente, a respost