Em um conjunto de dados analisado pelo Centro de Consultoria Estatística do Instituto Politécnico da Universidade de Virgínia, foi pedido a um conjunto de indivíduos que realizasse determinada tarefa no computador. A resposta medida foi o tempo para completar a tarefa. O propósito do experimento era testar uma série de ferramentas facilitadoras desenvolvidas pelo Departamento de Ciência da Computação local. Havia dez indivíduos envolvidos. Atribuídos aleatoriamente, cinco receberam um procedimento-padrão que usa a linguagem Fortran para completar a tarefa. Os outros cinco completaram a tarefa usando as ferramentas facilitadoras. Os dados sobre os tempos para conclusão das tarefas são fornecidos a seguir. Assumindo que as distribuições das populações são normais e as variâncias são as mesmas para os dois conjuntos, apóie ou refute a suposição de que as ferramentas aumentam a velocidade com a qual cada tarefa pode ser realizada.
Passo 1
Falaii galerinha do Responde ai, tudo belezinha?

Este é um problema de duas amostras em que devemos testar a igualdade de duas médias relacionadas a duas populações e os desvios padrão da população são iguais, mas desconhecidos.
Seja seja, respectivamente, as médias da população para o procedimento padrão e a ferramenta de facilitação.
Precisamos testar
Considere o nível de significância
Passo 2
Realizamos um teste de duas amostras e a estatística de teste é
Que segue a distribuição sob Ho com graus de liberdade .
= média amostral para o procedimento padrão
= = média amostral para a ferramenta de facilitação
= desvio padrão da amostra para o procedimento padrão
= desvio padrão da amostra para a ferramenta de facilitação
, respectivamente, os tamanhos de amostra para procedimento padrão e ferramenta de facilitação.
= diferença entre as médias populacionais sob Ho
A região crítica é
onde é o ponto superior de distribuição de com 8 graus de liberdade /
Passo 3
Com base na tabela a seguir
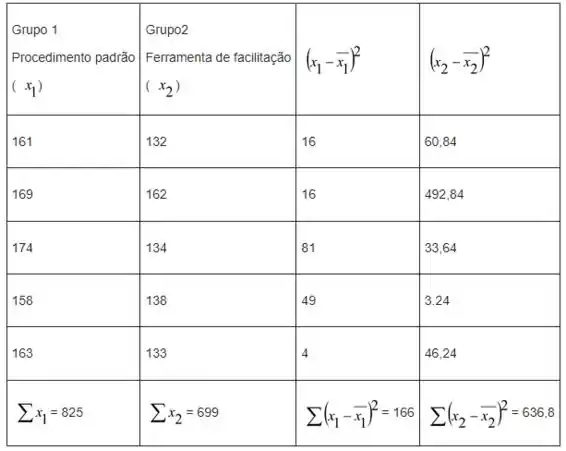
Temos
Então, nos teremos um valor observado
Passo 4
Então,
O valor tabelado de
Desta forma,
Portanto, rejeitamos apoiamos a conjectura de que as ferramentas de facilitação aumentam a velocidade com que a tarefa pode ser realizada.
Este é um teste unilateral. Portanto com 8 graus de liberdade.
Rejeitamos que Ha velocidade seja aumentada usando as regras de facilitação.
“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”

Resposta
Resposta nos passos.