Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 67

Sabemos que o volume dos recipientes de certo lubrificante é normalmente distribuído com variância de 0,03 litro. Teste a hipótese de que σ 2 = 0,03 contra a alternativa de que σ 2 ≠ 0,03 para uma amostra aleatória de dez recipientes do Exercício 10.25. Use um valor P em suas conclusões.

Passo 1

Falai galerinha, tudo certo:

Como diria a Viúva Negra, “Ainda somos amigos, certo?”

Boraaa fazer essa comigo

H 0 : σ 2 = 0.03

H 1 : σ 2 ≠ 0.03

Seja o nível de significância α = 0.0 1

Primeiro calculamos a variância da amostra para os dados fornecidos construindo a tabela a seguir

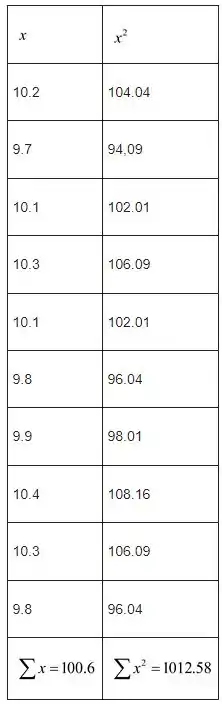
A variância da amostra é

s 2 = ∑ x 2 - ∑ x 2 n n - 1

= 1012.58 - 100.6 2 10 9

= 0.060444

Passo 2

Tamanho da amostra n = 10

A variação da população sob H 0   é   σ 2 = 0.03

A variação da amostra é s 2 = 0.060444

A estatística é

s 2 = n - 1 s 2 σ 0 2

= 10 - 1 × 0.060444 0.03

= 18.13333

x 2 = 18.13

Passo 3

O valor de P

Como este é um teste bicaudal, obtemos um valor de P aproximado determinando a área sob a curva de probabilidade qui-quadrado como v = n - 1 = 9 graus de liberdade, à direita da estatística do teste, onde x 2 = 18.13

P = 2 P x 2 ≥ 18.13

= 2 0.0337

= 0.0674

Decisão: O valor P é maior que o nível de significância, não rejeitamos H 0 . A amostra de 10 recipientes não é suficiente para mostrar que σ 2 não é igual a 0.03 .

“Nós somos Groot”

Resposta

Respostas nos passos.

Exercícios de Livros Relacionados

Para determinar as posições atuais sobre preces em escolas públicas, um experimento foi conduzido em quatro distritos do estado da Virgínia. A tabela a seguir contém as posições de 200 pais do distrit
No Exercício 9.88, use a distribuição t para testar a hipótese de que a dieta reduz o peso de uma pessoa em 4,5 quilogramas, em média, contra a alternativa de que a diferença média nos pesos é menor q
Dois tipos de instrumentos usados para medir a quantidade de monóxido sulfúrico na atmosfera estão sendo comparados em um experimento sobre poluição do ar. Deseja-se determinar se os dois tipos de ins
Em cem lançamentos de uma moeda, foram observadas 63 caras e 37 coroas. Essa moeda é balanceada? Use um nível de significância de 0,05.
Sabemos que as emissões de hidrocarboneto decresceram drasticamente durante os anos 1980. Um estudo foi conduzido para comparar as emissões de hidrocarboneto, em partes por milhão (ppm), para automóve