Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 89
No Exercício 1.19, teste a qualidade do ajuste entre freqüências de classes observadas e as freqüências esperadas na distribuição normal com ,, usando um nível de significância de 0,01.
Passo 1
Falai galerinha, tudo certo:
Como diria a Viúva Negra, “Ainda somos amigos, certo?”
Boraaa fazer essa comigo
Os dados a seguir representam a vida útil, em anos, de 30 bombas de combustível semelhantes:
O tamanho da amostra é n = 30.
Uma distribuição de frequência é
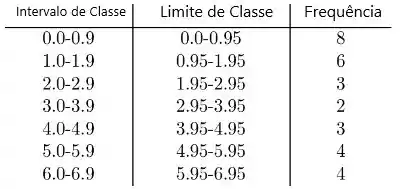
Precisamos testar a qualidade do ajuste entre as frequências de classe observadas e as frequências esperadas correspondentes de uma distribuição normal com , usando um nível de significância .
Assim, testamos a hipótese nula de que a vida útil das bombas de combustível pode ser aproximada por uma distribuição normal com média e desvio padrão .
Passo 2
Os valores z correspondentes aos limites apropriados das classes são:
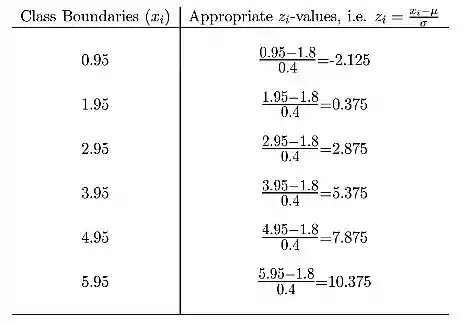
Passo 3
Nota: Vamos obter as frequências esperadas calculando as áreas sob a curva normal hipotética que se situam entre os vários limites de classe.
Por exemplo, na tabela anterior, vemos que os valores z correspondentes aos limites do segundo intervalo de classe (ou seja, a classe com limites 0,95 e 1,95) são Da Tabela A.3 encontramos a área entre
Observação2 Para o intervalo de primeira classe, usamos a área total sob a curva normal à esquerda do limite 0,95.
Para o último intervalo de classe, usamos a área total à direita do limite 5,95.
Todas as outras frequências esperadas são determinadas pelo método descrito para a segunda classe.
Assim, os limites z apropriados e as frequências esperadas são
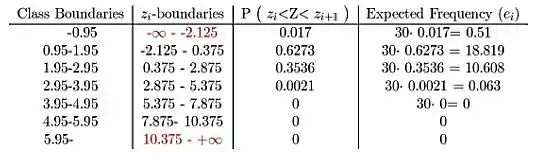
Passo 4
A tabela de frequências observadas e esperadas para cada intervalo de classe é,
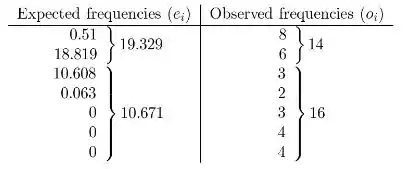
Observe que combinamos classes adjacentes na tabela anterior, porque as frequências esperadas são menores que 5 (uma regra prática no teste de qualidade do ajuste).
Consequentemente, o número total de intervalos é reduzido de 7 para 2, resultando em v = 1 grau de liberdade.
O valor de
Passo 5
Usando a Tabela A.5, encontramos para no liberdade = 1 grau de liberdade
Desde a . Para 1 grau de liberdade, não temos razão para rejeitar a hipótese nula.
Assim, concluímos que a distribuição normal com fornece um bom ajuste para a distribuição da vida útil das bombas de combustível.
A distribuição normal com fornece um bom ajuste para a distribuição da vida útil das bombas de combustível.
“Nós somos Groot”
Resposta
Respostas nos passos.