Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 101

Considere que uma balsa possa carregar tanto ônibus quanto carros em uma viagem por um canal. Cada viagem custa para o proprietário da balsa aproximadamente $ 10. A taxa para carros é $ 3 e, para ônibus, $ 8. Sejam e o número de ônibus e carros, respectivamente, levados em uma viagem. A distribuição conjunta de e é dada por

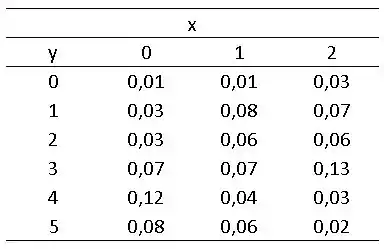
Calcule o lucro esperado para a balsa.

Passo 1

Falaa, meu querido/minha querida. Pelos dados do enunciado, podemos concluir que o lucro da balsa é representado pela variável aleatória abaixo:

Pois, cada viagem custa $10, mas traz $3 por cada um dos carros e $8 por cada um dos ônibus .

Portanto, o lucro esperado de pode ser descrito como:

Então, bora para os cálculos!!!

Passo 2

Como vimos no Passo 1, para encontramos o lucro esperado da balsa, devemos encontrar o valor esperado de e .

Encontrando o valor esperado de :

Encontrando o valor esperado de :

Portanto, o lucro esperado da balsa é dado por:

Resposta

Exercícios de Livros Relacionados

Calcule o coeficiente de correlação ρ de X e Y do Exemplo 5.16 (a covariância já foi calculada).

Annie e Alvie combinaram encontrar-se para almoçar juntos entre meio-dia e 13h. Represente por X a hora de chegada de Annie, por Y a de Alvie, e suponha que X e Y sejam independentes com fdps f X x =

Mostre que, se X e Y são vas independentes, então E X Y = E ( X ) ∙ E ( Y ) . Aplique essa expressão no Exercício 25. [Sugestão: considere o caso contínuo com f x ,y =f X x ∙ f Y ( y ) . ]

A diferença entre o número de clientes na fila da caixa expressa e o número de clientes na caixa superexpressa no Exercício 3 é X 1 - X 2 . Calcule a diferença esperada.

Considere uma pequena balsa que possa acomodar carros e ônibus. O pedágio para carros são US$ 3, e para ônibus, US$ 10. Sejam X e Y o número de carros e ônibus, respectivamente, levado em uma única vi