Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 63

Consulte o Exercício 3.

a. Calcule a covariância entre X1 = o número de clientes na caixa expressa e X2 = o número de clientes na caixa superexpressa.

b. Calcule V(X1 + X2). Como este valor se compara a V(X1) + V(X2)?

Passo 1

  1. Os valores esperados são

    2. E X 1 = 0 ∙ p X 1 0 + 1 ∙ p X 1 1 + 2 ∙ p X 1 2 + 3 ∙ p X 1 3 + 4 ∙ p X 1 4

    = 0 + 0.3 + 0.5 + 0.42 + 0.48

    = 1.7

    A pmf marginal de X 2 é

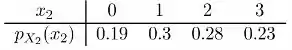
    O valor esperado é

    E X 2 = 0 ∙ 0.19 + 1 ∙ 0.3 + 2 ∙ 0.28 + 3 ∙ 0.23

    = 1.55

    A seguir estão os valores esperados da variável aleatória X 1 X 2

    E X 1 X 2 =   ∑ x 1 ∑ x 2 x 1 x 2 p x 1 , x 2 = 0 ∙ 0 ∙ 0.08 + 0 ∙ 1 ∙ 0.07 + … + 4 ∙ 2 ∙ 0.05 + 4 ∙ 3 ∙ 0.06 = 3.33

    A covariância é C o v X 1 , X 2 = E X 1 X 2 - E X 1 E X 2 = 3.33 - 2.635 = 0.695

    Passo 2

  2. Calculando as probabilidades

P X 1 = 4 = p x 1 4 = 0.12

P X 2 = 0 = p x 2 0 = 0.19

P X 1 = 4 ,   X 2 = 0 = p 4,0 = 0

Note que

p 4,0 = 0   ≠ 0.0228 = 0.12 ∙ 0.19 = p x 1 4 ∙ p x 2 0

a partir do qual podemos concluir que as variáveis aleatórias são dependentes.

Como as variáveis aleatórias são dependentes, a igualdade

V X 1 + X 2 = V X 1 + V X 2

  não fica! Em vez disso, use a seguinte igualdade para calcular a variância

V X 1 + X 2 = V X 1 + V X 2 + 2 C o v X 1 ,   X 2

e para variável aleatória X 2

Por fim, vale o seguinte

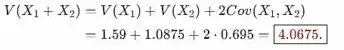
Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

(a) Mostre que a variância amostrai não muda seuma constante c for adicionada ou subtraída de cada valor na amostra.(b) Mostre que a variância amostrai se torna c2 vezesseu valor original, se cada obs
Uma amostra de tamanho 25 é retirada de uma população normal que tem média 80 e desvio-padrão 5.Uma segunda amostra aleatória de tamanho 36 é retiradade outra população normal com média 75 e desvio-pa
Duas máquinas diferentes são utilizadas para enchercaixas de cereais em uma linha de produção. A mediçãocrítica influenciada por essas máquinas é o peso do produto nas máquinas. Engenheiros têm quase
Se Sf e Sí representam as variâncias de amostrasaleatórias independentes de tamanho n} = 8 e n, = 12,retiradas de populações normais com variâncias iguais,determine P(S]ISf
(a) Determine /()(p. quando v = 14.(b) Determine -t{)I0 quando v = 10.(c) Determine í0995 quando v=7.