Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 9a
Dada à distribuição conjunta de e Y abaixo, determine a média e a variância de:
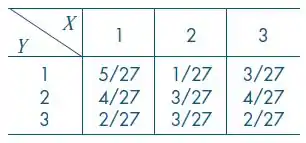
Passo 1
Sabemos que:
Assim,
Passo 2
Além disso, sabemos que:
Assim,
Finalmente,
Portanto,
Resposta
Exercícios de Livros Relacionados
Use o Teorema 4.7 para avaliar E ( 2 X Y 2 - X 2 Y ) para a distribuição de probabilidade conjunta mostrada na Tabela 3.1.
Suponha que X e Y sejam variáveis aleatórias independentes com densidades de probabilidade g x = 8 x 3 , x2 0 ,c a s oc o n t r á r i o á E h y = 2 y , 0y1 0 ,c a s oc o n t r á r i o á Determine o va
Sejam X o número que ocorre quando um dado vermelho é jogado e Y , o número que ocorre quando um dado verde é jogado. Determine(a) E ( X + Y ) ;(b) E ( X - Y ) ;(c) E ( X Y ) .
Suponha que você jogue um dado, não adulterado, de dez lados (0, 1, 2, ..., 9) 500 vezes. Usando o teorema de Chebyshev, calcule a probabilidade de que a média amostral, X , esteja entre 4 e 5.
Prove o teorema de Chebyshev quando X for umavariável aleatória discreta.