Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 59

Use o Teorema 4.7 para avaliar E ( 2 X Y 2 - X 2 Y ) para a distribuição de probabilidade conjunta mostrada na Tabela 3.1.

Passo 1

Falaa, meu querido/minha querida. A distribuição de probabilidade conjunta das variáveis aleatórias discretas X e Y é:

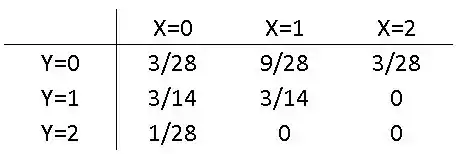
Então, bora para os cálculos!!!

Passo 2

Usando a regra E g X ,   Y + h X ,   Y = E g X ,   Y + E h X ,   Y combinada com a regra E a X = a E ( X ) , nós temos:

E 2 X Y 2 - X 2 Y = 2 E X Y 2 - E ( X 2 Y )

= 2 ∑ x ∑ y x y 2 f ( x ,   y ) - ∑ x ∑ y x 2 y f ( x ,   y )

= 2 ∑ x = 0 2 ∑ y = 0 2 x y 2 f ( x ,   y ) - ∑ x = 0 2 ∑ y = 0 2 x 2 y f ( x ,   y )

Aqui, podemos remover os somatórios para quando x = 0 ou y = 0 , pois, resultariam em x y 2 = x 2 y = 0 e não irão contribuir no somatório.

= 2 ∑ x = 1 2 ∑ y = 1 2 x y 2 f ( x ,   y ) - ∑ x = 1 2 ∑ y = 1 2 x 2 y f ( x ,   y )

Por fim, iremos aplicar apenas os somatórios onde f x , y ≠ 0 .

= ( 2 ) 1 1 2 f 1 ,   1 - 1 1 f ( 1 ,   1 )

= 1 1 3 14

E 2 X Y 2 - X 2 Y = 3 14

Resposta

E 2 X Y 2 - X 2 Y = 3 14

Exercícios de Livros Relacionados

Uma variável aleatória X tem a seguinte distribuição de probabilidades: f X ( x ) = e - x , x ≥ 0 Encontre a distribuição de probabilidades para Y=X^2Encontre a distribuição de probabilidades para Y=X
Suponha que X seja uma variável aleatória contínua com distribuição de probabilidades f X ( x ) = x 18 ,0 ≤ x ≤ 6 Encontre a distribuição de probabilidades da variável aleatória Y=2X+10Encontre o valo
Suponha que X tenha uma distribuição de probabilidades uniformes f X ( x ) = 1 ,0 ≤ x ≤ 1 Mostre que a distribuição de probabilidades da variável aleatória Y= -2lnX é uma variável qui-quadrado com doi
Na fabricação de lâmpadas de eletroluminescência, para as camadas diferentes de tinta são depositadas em um substrato plástico. A espessura dessas camadas é crítica se especificações relativas a cor f
Se X e Y têm uma distribuição normal bivariada com rho =0, mostre que X e Y são independentes