A presença de carbetos de liga dura em ligas de ferro de cromo branco alto produz uma excelente resistência à abrasão, o que as torna adequadas à manipulação de materiais na mineração e às indústrias de processamento de materiais. Os dados a seguir sobre x volume de austenita x retida (%) e y perda de resistência abrasiva (mm3 ) em testes de desgaste de pinos usando a granada como abrasivo foram reproduzidos de um gráfico apresentado no artigo “Microstructure Property Relationships in High Chromium White Iron Alloys” (Intl. Materials Reviews, 1996, p. 59–82).
Use os dados e o resultado SAS a seguir para responder às perguntas da próxima página
a. Que proporção de variação observada na perda de resistência abrasiva pode ser atribuída à relação do modelo de regressão linear simples? b. Qual é o valor do coeficiente de correlação amostral? c. Teste a utilidade do modelo de regressão linear simples usando 0,01. d. Estime a perda média real por desgaste quando o volume é 50%. Faça os cálculos de maneira que transmitam informações sobre confiabilidade e precisão. e. Que valor de perda por desgaste você preveria com um volume de 30% e qual é o valor do resíduo correspondente?
Passo 1
Usaremos o seguinte:
A regressão linear é uma equação linear de duas variáveis das quais uma é independente e uma é dependente da outra. Seja X uma variável independente e Y uma variável dependente. A equação linear é definida por:
Onde são os coeficientes.
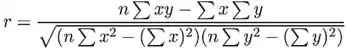
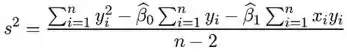
Para testar hipóteses vs nós iremos usar a próxima estatística:
nesta tarefa temos os dados sobre a taxa de consumo de óleo diesel medida pelo método do peso de drenagem (x) e a taxa medida pelo método CI-trace (y). Os dados são dados abaixo: Os dados são: 
Passo 2
- Agora precisamos testar as hipóteses Então, para isso, precisamos calcular os próximos valores:
- Na subseção anterior (a) calculamos que o coeficiente de correlação é igual a 0,97. Isso significa que existe uma forte relação linear positiva entre essas duas variáveis.
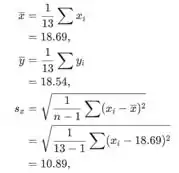

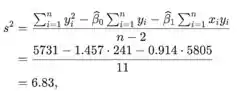
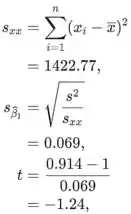
Passo 3
Como t é maior que -t.krit, aceitamos hipóteses nulas e é 1.
Resposta
Ver o desenvolvimento.