Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 59
Em determinado posto de gasolina, 40% dos clientes usam gasolina comum (), 35% usam gasolina aditivada () e 25% usam gasolina premium (). Dos clientes que usam gasolina comum, apenas 30% enchem o tanque (evento B). Dos clientes que usam gasolina aditivada e premium, 60% enchem o tanque, enquanto dentre os que usam premium, 50% enchem
o tanque.
a) Qual é a probabilidade de o próximo cliente pedir gasolina aditivada e encher o tanque
b) Qual é a probabilidade de o próximo cliente encher o tanque?
c) Se o próximo cliente encher o tanque, qual é a probabilidade de pedir gasolina comum? E gasolina aditivada? E gasolina premium?
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Vamos fazer um esquema para facilitar o entendimento do enunciado.
);
);
).
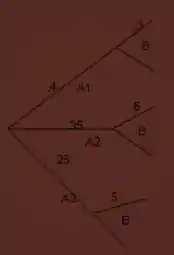
Vamos começar resolvendo o item a)
Como já calculamos,
Passo 2
Vamos ao item b)
Nesse item queremos calcular .
Para fazermos isso iremos somar os três “trechos” que nos levam a B e assim encontraremos .
Vamos aos cálculos:
Passo 3
Agora, partindo ao item c)
Nesse item estamos interessados no caso em que “se o próximo cliente encher o tanque, qual é a probabilidade de pedir gasolina comum? E gasolina aditivada? E gasolina premium?”
Vamos traduzir isso para o “matematiquês”, teremos assim:
E fazendo a segunda parte do item c), chegamos em:
E por fim a terceira parte, usando o complementar, temos:
Resposta
a)
b)
c)