Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 14
Os relês fabricados pela empresa A têm duração média de 1.400 h e desvio padrão de 200 h, enquanto que os da empresa B têm duração média de 1.200 h e desvio padrão de 100 h. Se forem ensaiadas amostras aleatórias de 125 relês de cada marca, qual é a probabilidade das de marca A terem vida média superior que as de B de pelo menos:
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.
A distribuição amostral de somas ou diferenças com duas médias amostrais, com desvios padrões populacionais conhecidos. Onde o score reduzido é:
Pelo enunciado temos os seguintes dados:
- ;
- ;
- ;
- ;
- .
E queremos saber a probabilidade da empresa A ter vida média superior que as de B ():
- para o item a) queremos de pelo menos 160 h:
- e para o item b) queremos de pelo menos 250 h:
Pela tabela da distribuição normal é:
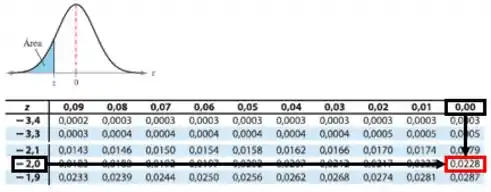
Passo 2
Pela tabela da distribuição normal é:
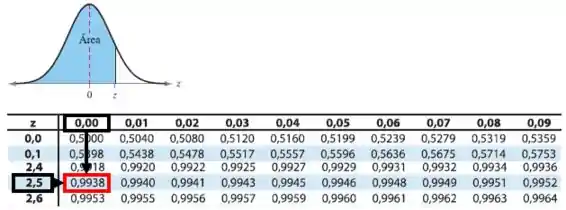
Tchau galerinha! Te espero em mais exercícios.
Resposta
- .
- .