Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 36
Determine a cor variância e a correlação para distribuição de probabilidade de conjuntos mostrados na figura 5.4 e descrito no exemplo se.6
Passo 1
A distribuição de probabilidade conjunta do exemplo de exercício é:
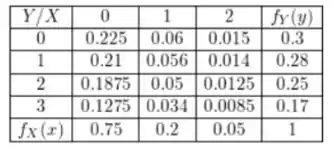
Para calcular a covariância, vamos usar:
E para correlação,
Passo 2
Como a covariância é 0, isso implica que o coeficiente de correlação também é 0. Portanto, as 2 variáveis aleatórias são independentes.
Resposta
Exercícios de Livros Relacionados
Dada a função de densidade conjunta f x , y = 6 - x - y 8 ,0x2 , 2y4 0 , c a s oc o n t r á r i o á Determine P ( 1Y3 | X = 1 ) .
Cada pneu traseiro de um avião experimental precisa ser enchido com uma pressão de 40 libras (1 libra = 4 54 gramas) por polegada quadrada (psi – libra por polegada quadrada). Considere X a pressão at
A quantidade de querosene, em milhares de litros, em um tanque, no início de qualquer dia, é uma quantidade aleatória K, da qual uma quantidade aleatória X é vendida por dia. Suponha que o tanque não
Um serviço de facilidades opera com duas linhas de serviço. Em um dia selecionado aleatoriamente, considere X a proporção do tempo no qual a primeira linha é usada e Y a proporção do tempo no qual a s
Uma empresa de tabaco produz misturas com diversas proporções de tabaco turco, doméstico e outros. A proporção de tabaco turco e doméstico em uma mistura são as variáveis aleatórias com função de dens