Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 34

Determine a covariância e a correlação para a seguinte distribuição de probabilidades conjuntas

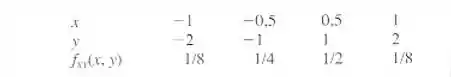
Passo 1

A distribuição dada de probabilidade conjunta para X e Y é:

Para obter a covariância e correlação entre X e Y, usamos:

c o v ( X , Y ) , σ x y = E ( X Y ) - E ( X ) E ( Y ) =

= ρ x y = c o v ( X , Y ) V ( X ) V ( Y ) =

= σ x y σ x σ y

Passo 2

Primeiro, vamos determinar os valores de E ( X ) ,   E ( Y )   e   E ( X , Y ) :

E ( X ) = 0.125

E ( Y ) = 0.25

E ( X , Y ) = 0.875

Passo 3

Agora vamos encontrar os valores de V ( X )   e   V ( Y ) :

V ( X ) = 0.421875

V ( Y ) = 1.6875

Passo 4

Agora, podemos encontrar os valores de c o v ( X , Y )   e   ρ ( X , Y ) :

c o v ( X , Y ) = 0.84375

ρ x y = c o v ( X , Y ) V ( X ) V ( Y ) = 1

Resposta

c o v ( X , Y ) = 0.84375

ρ x y = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se as duas variáveis aleatórias do Exercício 3.43 são dependentes ou independentes.
Considere a seguinte função de densidade de probabilidade conjunta para as variáveis aleatórias X e Y : f x ,y = 3 x - y 91x3 ,1y2 0 , c a s oc o n t r á r i o á (a) Determine as funções de densidade
Dois componentes eletrônicos do sistema de um míssil funcionam em harmonia para o sucesso total do sistema. ConsidereX e Y a vida, em horas, dos dois componentes. A densidade conjunta de X e Y é f x ,
Considere X , Y e Z com a seguinte função de densidade de probabilidade conjunta f x ,y = k x y 2 z ,0x , y1 ,0z2 0 ,c a s oc o n t r á r i o á (a) Determine k .(b) Determine P ( X1 4 , Y1 2 , 1Z2 ) .
Determine se as duas variáveis aleatórias do Exercício 3.44 são independentes ou não.