Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 28b
Na distribuição encontre:
(b)
Passo 1
Mais uma vez lembrando que quando temos uma variável com distribuição normal, precisamos utilizar uma aproximação para a forma padrão dessa variável; é assim:
Quando tivermos uma probabilidade, teremos o seguinte:
Passo 2
Agora, na alternativa B, vamos ter de abrir o módulo,
E então:
Isso significa que a nossa aproximação vai ser algo do tipo:
Logo, vamos buscar:
Se lembrarmos que o gráfico é simétrico, podemos denotar o seguinte:
Então podemos dizer que:
Passo 3
Ou seja, só precisamos buscar na tabela de distribuição normal, o valor de :
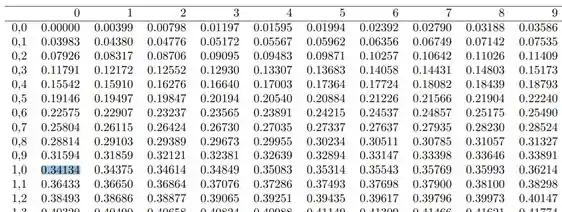
Portanto:
Podemos concluir:
Resposta
(b)
Exercícios de Livros Relacionados
O período de hospital, em dias, para pacientes em tratamento para certo tipo de problema renal é a variável aleatória Y =X +4 , onde X tem a seguinte função de densidade f x = { 32 x + 4 3 , x00 , c a
No Exercício 3.29, estávamos lidando com a distribuição do tamanho de uma importante partícula, com a distribuição do tamanho da partícula caracterizada por f x = { 3 x - 4 , x10 , c a s oc o n t r á
A função densidade de uma variável aleatória X tem como gráfico a figura abaixo (lei de Simpson). Achar as expressões das funções densidade e distribuição, bem como calcular a esperança matemática, o
Calcular: P 1 ≤ x ≤ 2 , para a variável aleatória X que segue a distribuição uniforme no intervalo 1 2a3 2 .
Suponha que o seu médico recomende-lhe seguir um regime especial de emagrecimento durante quatro semanas. Levando em conta a sua constituição física, ele considera que o peso que o cliente pode perder