No Exercício 3.29, estávamos lidando com a distribuição do tamanho de uma importante partícula, com a distribuição do tamanho da partícula caracterizada por
(a) Represente a função de densidade.
(b) Dê o tamanho médio da partícula.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro vamos representar a função de densidade graficamente, desse modo, ficaremos com:
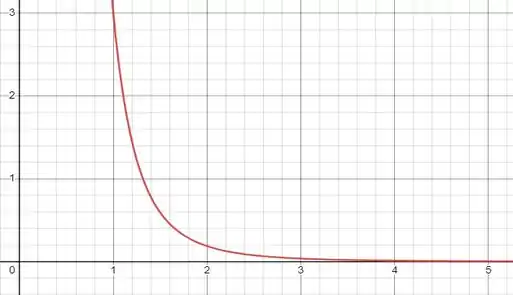
Passo 2
Agora vamos ao item b)
Queremos o tamanho médio da partícula.
Lembrando que o valor esperado é dado pela seguinte relação:
Vamos dividir essa integral em dois intervalos e aplicar a função densidade de probabilidade nesses intervalos. Assim:
Desse modo:
Resolvendo essa integral, podemos concluir que
Resposta
- Vide gráfico