Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 4.Exercícios propostos - Ex. 15

A função densidade de uma variável aleatória X tem como gráfico a figura abaixo (lei de Simpson). Achar as expressões das funções densidade e distribuição, bem como calcular a esperança matemática, o desvio padrão e a probabilidade de X estar entre 0,5   e   0,7 .

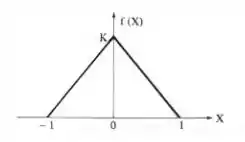
Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro do Mauri guerra de estática indutiva A função densidade de uma variável aleatória X tem como gráfico a figura abaixo (lei de Simpson). Achar as expressões das funções densidade e distribuição, bem como calcular a esperança matemática, o desvio padrão e a probabilidade de X estar entre 0,5   e   0,7 .

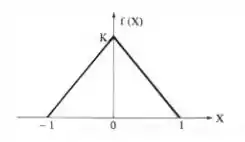
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Para determinarmos o desvio padrão e a probabilidade de X temos,

f x = 0 ,     p a r a   x ≤ - 1 x + 1 ,     p a r a   - 1 < x ≤ 1 1 - x ,     p a r a   0 ≤ x ≤ 1 0 ,     p a r a   x > 1     e           f x = 0 ,     p a r a   x ≤ - 1 x + 1 2 2 ,     p a r a   - 1 < x ≤ 0 1 - 1 - x 2 2 ,     p a r a   0 < x ≤ 1 1 ,     p a r a   x > 1

Ficando,

μ = 0 ,     σ = 0,41 ,     P 0,5 ≤ x ≤ 0,7 = 8 %

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

μ = 0 ,     σ = 0,41 ,     P 0,5 ≤ x ≤ 0,7 = 8 %

Exercícios de Livros Relacionados

Se a variável aleatória X é definida de modo que E X - 1 2 = 10 ,E X - 2 2 = 6 , Determine μ e σ 2 .
Considere X uma variável aleatória com probabilidade/ w = í i ’ x = 1 , 2 , 3 \[0, caso contrario.Determine a distribuição de probabilidade da variávelaleatória Y = IX - 1.
Dada a variável aleatória X com distribuição de probabilidadef(x) = [ 2x' 0 J \0, caso contrário,determine a distribuição de probabilidade de Y = SX3
Uma variável aleatória X tem distribuição de Poisson p{x; //) = e~f( ffh à para x = 0, 1 , 2, ... Mostre que afunção geradora de momentos é Usando MÁt) determine a média e a variância da distribuição
O lucro de um revendedor, em unidades de $ 5.000,em um novo automóvel é dado por Y = X2, onde X éuma variável aleatória com função de densidade2 ( 1 - x), 0 caso contrário.(a) Determine a função de de