Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 28c
Na distribuição encontre:
- O número tal que
Passo 1
Novamente, vamos ter:
E
Passo 2
Na alternativa C, vamos aproximar da seguinte forma:
E facilmente:
Lembrando sempre que como o gráfico é simétrico, vamos ter o seguinte:
E podemos dizer que:
Passo 3
Isso significa que precisamos buscar, na tabela de distribuição normal, um valor tal que:
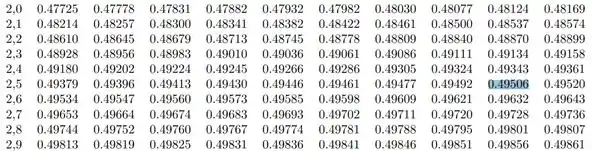
Encontramos que:
Portanto,
Resposta
(c)
Exercícios de Livros Relacionados
Num laboratório, se um equipamento está funcionando, a função de densidade do resultado observado,X ,é f x = 2 1 - x , 0x1 0 , c a s oc o n t r á r i o á Determine a variância e o desvio-padrão de X .
O tempo total, medido em unidades de cem horas, no qual uma adolescente usa seu aparelho de som durante o período de um ano, é a variável aleatória que tem função de densidade f x = x , 0x1 2 - x , 1
Seja X a variável aleatória com a seguinte distribuição de probabilidade:Determine E ( X ) e E ( X 2 ) e, então, usando esses valores, avalie E [ 2 X + 1 2 ] .
Repita o Exercício 4.43, aplicando os teoremas 4.5 e 4.9.
Se a variável aleatória X é definida de modo que E X - 1 2 = 10 ,E X - 2 2 = 6 , Determine μ e σ 2 .