Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 28d
Na distribuição encontre:
- O número tal que
Passo 1
Uma última vez, sempre lembrando:
E quando tivermos uma probabilidade, teremos o seguinte:
Passo 2
Na alternativa D, basta usar a aproximação e vamos chegar no seguinte:
Se você se lembrar, cada metade do gráfico possui probabilidade igual a 0,5; perceba então que se utilizarmos , teremos:
E pela simetria do gráfico,
Isso significa que somente precisamos buscar um , tal que:
Passo 3
Buscando isso na tabela de distribuição normal, chegamos no seguinte:
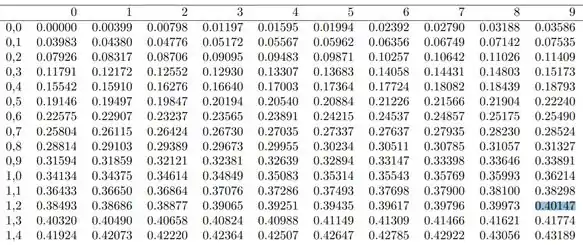
Então, devido a simetria do gráfico:
Portanto,
Finalmente encontramos que:
Resposta
(d)
Exercícios de Livros Relacionados
Considere X uma variável aleatória com probabilidade/ w = í i ’ x = 1 , 2 , 3 \[0, caso contrario.Determine a distribuição de probabilidade da variávelaleatória Y = IX - 1.
Dada a variável aleatória X com distribuição de probabilidadef(x) = [ 2x' 0 J \0, caso contrário,determine a distribuição de probabilidade de Y = SX3
Uma variável aleatória X tem distribuição de Poisson p{x; //) = e~f( ffh à para x = 0, 1 , 2, ... Mostre que afunção geradora de momentos é Usando MÁt) determine a média e a variância da distribuição
O lucro de um revendedor, em unidades de $ 5.000,em um novo automóvel é dado por Y = X2, onde X éuma variável aleatória com função de densidade2 ( 1 - x), 0 caso contrário.(a) Determine a função de de
O período de internação, em dias, para pacientes quefazem tratamento para certo tipo de doença renal é umavariável aleatória Y- X + 4, onde X tem função densidadef(x ) = x0,caso contrário.(a) Determin