Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 30b

Um teste de aptidão feito por pilotos de aeronaves em treinamento inicial requer que uma série de operações seja realizada em uma rápida sucessão.

Suponha que o tempo necessário para completar o teste seja distribuído de acordo com uma normal de média 90   m i n u t o s   e desvio padrão de 20   m i n u t o s .

(b) Se os 5% melhores são alocados para aeronaves maiores, quão rápido deve ser o melhor candidato para que obtenha essa posição?

Passo 1

Antes de tudo, vamos definir nossas variáveis:

X = T e m p o   p a r a   c o m p l e t a r   o   t e s t e   e m   m i n u t o s .

E

Y = Q u a n t i d a d e   d e   a p r o v a d o s .

Perceba que,

X ~ N 90   ; 20 2

Enquanto:

Y ~ B i n o m i a l ( n ; p )

Passo 2

(b) P X < t = 0,05

Fazendo aproximação pela normal padrão:

P X < t = P Z < t - 90 20 = 0,05

Se chamarmos

- z = t - 90 20

Precisamos buscar na tabela um valor tal que:

P - ∞ < Z ≤ 0 - P - z ≤ Z ≤ 0 = P Z < - z = 0,05

Então:

P 0 ≤ Z ≤ z = 0,5 - 0,05 = 0,45

Passo 3

Da tabela:

P 0 ≤ Z ≤ 1,64 = 0,45

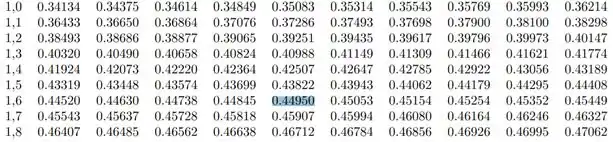
Ou seja:

- 1,64 = t - 90 20

Isolando t :

t = 57,2   m i n u t o s

Resposta

Concluimos que o melhor candidato deve concluir a prova em menos de 57,2 minutos para estar entre os 5 % melhores.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja X ~ N 5,4 . Determine:(a) P X ≤ 6 .
Seja X ~ N 5,4 . Determine:(b)P 7X8 .
Seja X ~ N 5,4 . Determine:(c) P 2 ≤ X5
Seja X ~ N 5,4 . Determine:(d) P - 1 ≤ X ≤ 2
Ao expandir e lxem uma série de MacLaurin e integrando termo a termo, mostre queM x(t) dxt= 1 + flt+ ft2-^, + - + Jtr-y +r\