Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 65

Doze refrigeradores de um determinado tipo foram devolvidos ao distribuidor por causa de um ruído audível, oscilante e agudo que faziam quando em funcionamento. Suponha que sete desses refrigeradores possuam um compressor defeituoso e os outros cinco tenham problemas graves. Se os refrigeradores forem examinados em ordem aleatória, seja X o número de refrigeradores examinados entre os seis primeiros com compressores defeituosos. Calcule os seguintes valores: a. P(X 5) b. P(X 4) c. A probabilidade de X exceder o valor da média em mais de 1 desvio padrão. d. Considere uma entrega de 400 refrigeradores, dos quais 40 possuem compressores com defeito. Se X for o número de compressores defeituosos entre 15 refrigeradores selecionados aleatoriamente, descreva uma forma menos cansativa de calcular (ao menos aproximadamente) P(X 5) em vez de usar a fmp hipergeométrica. Enunciado aqui

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Dado:

N = T a m a n h o   d a   p o p u l a ç ã o = 12

n = N u m e r o   d e   d e s e n h o s = 6

r = N u m e r o   d e   s u c e s s o s = 7

Como uma população finita foi dada, precisamos usar a distribuição hipergeométrica.

Probabilidade hipergeométrica da fórmula:

p y = r y N - r n - y N n

Passo 2

  1. Para y = 5

    2. P X = 5 = p 5 =   7 5 12 - 7 6 - 5 12 6 = 5 44 = 11.36 %

  2. Avalie a fórmula em y=0,1,2,3,4:

    3. p 0 = 0

    Nota: A probabilidade é zero, porque o evento é impossível (quando não há sucessos, então precisa haver 6 falhas, mas temos apenas 5 falhas na população).

    Regra de adição para eventos disjuntos ou mutuamente exclusivos:

    P A   o u   B = P A + P B

    Adicione as probabilidades correspondentes:

    P   X   ≤ 4   = p 0 + p 1 + p 2 + p 3 + p 4

    = 0 + 1 132 + 5 44 + 25 66 + 25 66 = 116 132 = 29 33 = 87.88 %

    Passo 3

  3. A média da distribuição hipergeométrica é o produto do número de sucessos e do número de empates, dividido pelo tamanho da população:

    4.   μ = r n N = 6 7 12 = 7 2 =   3.5

    O desvio padrão da distribuição hipergeométrica é então:

    σ =   r n N ∙ N - r N ∙ N - n N - 1 =   6 7 12 ∙ 12 - 6 12 ∙ 12 - 7 12 - 1 = 0.8919

    Determine os valores que são um desvio padrão da média:

    μ -   σ = 3.5 - 0.8919 = 2.6081

    μ + σ = 3.5 + 0.8919 = 4.3919

    Precisamos determinar a probabilidade de X ser mais de um desvio padrão acima da média e, portanto, a probabilidade de X ser maior que 4.

    Regra do complemento:

    P n a o   A = 1 - P A

    Use a regra do complemento e o resultado da parte (b):

    P X >   μ + σ = P X > 4 = 1 - P X   ≤ 4 = 1 - 29 33 = 4 33 = 12.12 %

  4. Dado:

N = t a m a n h o   d a   p o p u l a ç ã o = 400

n = n u m e r o   d e   d e s e n h o s = 15

r = n u m e r o   d e   s u c e s s o s = 40  

Como a amostra de 15 é muito menor que o tamanho da população N=400N=400, podemos supor que todos os itens da população são independentes e que sorteamos os itens com reposição.

Podemos então aproximar a distribuição hipergeométrica pela distribuição binomial com n=15n=15 e probabilidade de sucesso p = r N = 40 400 = 1 10 = 0.1

Definição de probabilidade binomial:

Avaliando para k = 0,1 , 2,3 , 4,5 :

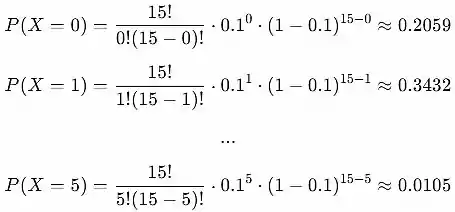
Regra de adição para eventos disjuntos ou mutuamente exclusivos:

P A   o u   B = P A + P B

Adicione as probabilidades correspondentes:

P X   ≤ 5   = P X = 0 + P X = 1 + … + P X = 5

= 0.2059 + 0.3432 + … + 0.0105 = 0.9978 = 98.78 %

Resposta

  1. 11.36 %
  2. 87.88 %
  3. 12.12 %
  4. 99.78 % %

Exercícios de Livros Relacionados

Suponha que X tenha uma distribuição hipergeométrica com N = 10 ,n = 3 e K =- 4 . Esquematize a função de probabilidade de X . Determine a função de distribuição cumulativa para X
Fita magnética é cortado em pedaços, com uma largura de meia polegada, que são enrolados em cartuchos. Um arranjo contém 48 lâminas. Cinco lâminas são selecionadas ao acaso avaliadas a cada dia em rel
Calcule as correções para população finita para os exercícios 3-97 e 3-98. Para qual exercício, a aproximação binomial para distribuição de X deveria ser melhor? Para o exercício 3.97 calcule, conside
O diâmetro X de um cabo elétrico supõe-se ser uma variável aleatória continua X, com fdp: f x = 6 x 1 - x ,0 ≤ x ≤ 1 Verifique que essa expressão é uma fdp e esboce o seu gráfico, obtenha uma expressã
Seja X a duração da vida (medida em horas) de um dispositivo eletrônico. Suponha que X seja variável aleatória contínua com fdp f x = k x n ,2000 ≤ x ≤ 10000 . P a r an = 2 ,d e t e r m i n ek .